Атомы с двумя и более электронами в верхней оболочке (Раздел 1.2. учебного пособия)

1.2. Атомы с двумя и более электронами в верхней оболочке

Главный физический фактор, обуславливающий специфику свойств многоэлектронных атомов, сводится к доминирующей роли многочастичных взаимодействий. При этом основную роль играют два обстоятельства: тождественность электронов, приводящая к наличию обменного взаимодействия, и наличие спина, влияющего на симметрию пространственной волновой функции.

В качестве примера, рассмотрим простейшую многоэлектронную систему — атом гелия [2,3]. При решении будем использовать методы теории возмущений. Как было показано ранее (5), в нулевом приближении волновая функция Hе есть произведение волновых функций:

,                                         (16)

где   — соответственно, волновые функции первого и второго электронов, находящихся в состоянии a и b с собственными значениями энергий  и .

В соответствии с принципом Паули, волновая функция должна отвечать определенным принципам симметрии. В частности, для частиц с полуцелым спином () осуществляются лишь состояния с антисимметричными полными волновыми функциями.

Учитывая тождественность электронов и наличие у них спина, можно построить четыре антисимметричных функции:

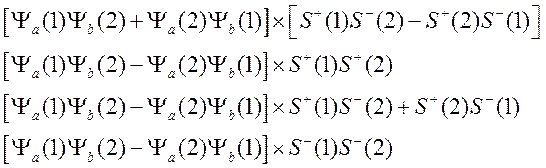;(17)

где  и  — спиновые волновые функции 1-го и 2-го электронов, имеющие собственные значения , т.е. .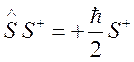

Первая волновая функция в (17) соответствует синглетному состоянию со спином атома S = 0. Следующие три функции описывают состояние с полным спином S = 1 (триплетное состояние, названное так по величине мультиплетности 2S + 1 = 3). Каждая из этих функций соответствует различным проекциям M_s (+1,0,-1).

В соответствии со стационарной теорией возмущений, поправка к энергии определяется выражением:

,                                              (18)

где интегрирование осуществляется по координатам обеих частиц, а 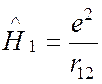 — энергия взаимодействия между электронами. Энергия возмущения не зависит от спиновых функций и в выражении (18) под  можно подразумевать только координатную часть функции. Существенно отметить, что координатные части возможных значений  в (17), описывающих состояния системы, выражаются как через антисимметричные, так и симметричные решения уравнения Шредингера.

Поправку к энергии (18) можно представить в виде [2,3]:

 при ,                                     (19)

причем знак плюс относиться к синглетному состоянию (спины электронов антипараллельны и полный спин равен нулю), а знак минус к триплетному состоянию;

 при (a = b),                                  (19’)

в этом случае возможно только синглетное состояние атома с антипараллельными спинами отдельных электронов.

В (19) использованы обозначения:

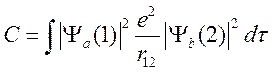,                                 (20)

.

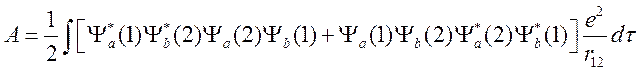Интеграл С определяет среднюю кулоновскую энергию взаимодействия между электронными облаками. Интеграл А связан с идентичностью электронов и его обычно называют “обменным”.

Полная энергия атома гелия равна:

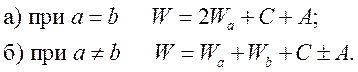                                                             (21)

Напомним, что  и  отрицательны, A и С всегда положительны, а знак перед А определяется ориентацией спина.

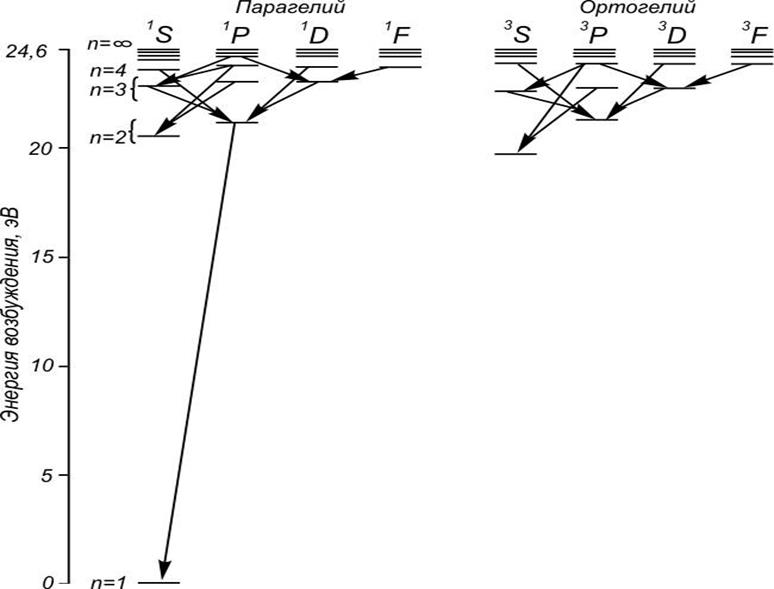
Изложенная структура энергетических состояний подтверждается экспериментально. На рис. 2 приведена схема энергетических уровней Не, распадающихся на синглетные и триплетные состояния. Состояние  отсутствует, в полном соответствии с (19’).

Как мы уже отмечали, в нулевом приближении энергия связи каждого электрона равна 54,40 эВ. При учете электростатического взаимодействия электронов имеем энергию связи  электронов 24,6 эВ, т.е. поправка С + А в этом случае равна 29,8 эВ. Ее нельзя рассматривать малой и, строго говоря, применение теории возмущений не оправдано. Необходимы более точные методы расчета. Величину поправки A (обменное взаимодействие) можно оценить, например, по разности синглетного и триплетного уровней при n = 2. Из рис. 2 видно, что  эВ. Такой же масштаб (при n = 2) имеет изменение С + А  при изменении .

Таким образом, на примере анализа энергетических состояний атома Не с двумя электронами показано, что наличие электростатического взаимодействия между электронами , а также учет идентичности электронов и требований симметрии волновых функций приводят: во-первых, к смещению энергетических уровней, причем значение смещения, определяемое, в основном, величиной поправки С (cм.(20)) зависит от орбитального момента  электронов; во-вторых, к расщеплению энергетических уровней в зависимости от ориентации их спинов. Следовательно, снимается вырождение по величине  L и  S, однако, энергия атома не зависит от ориентации  и  т.е. остается вырождение по величине и направлению полного момента . Очевидно, что данные выводы применимы и к атомам

со многими электронами.

Существует несколько приближенных методов расчета энергетических состояний сложных атомов (вариационный, методы Слетера, Хартри и Фока, Томаса-Ферми) [1,3]. Они не изменяют изложенные выше общие закономерности и здесь мы на них останавливаться не будем.