![]() ,
(52)
,
(52)
умножив на ![]() и проинтегрировав по всему пространству,
получим
и проинтегрировав по всему пространству,
получим
![]() . (53)
. (53)
Учитывая,
что ![]() равна (49,50), а каждая из
равна (49,50), а каждая из ![]() и
и ![]() являются
волновыми функциями основного состояния атома водорода, получим
являются
волновыми функциями основного состояния атома водорода, получим
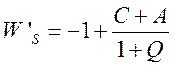 и
и 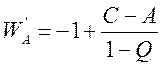 ,
(54)
,
(54)
где  — кулоновский интеграл,
— кулоновский интеграл,
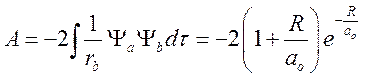 — обменный интеграл.
— обменный интеграл.
Для нахождения полной энергии молекулы ![]() мы
должны прибавить потенциальную энергию взаимодействия двух протонов в единицах Rp
:
мы
должны прибавить потенциальную энергию взаимодействия двух протонов в единицах Rp
: ![]() . Таким образом, имеем:
. Таким образом, имеем:
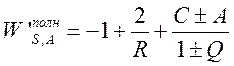 .
(55)
.
(55)
Графики зависимости Еполн. от ![]() представлены на рис. 13 использованы
обозначения
представлены на рис. 13 использованы
обозначения ![]() и
и ![]() . В
симметричном случае получаем энергию связи 0,13
. В
симметричном случае получаем энергию связи 0,13 ![]() (1,8
эВ) при равновесном состоянии R =
(1,8
эВ) при равновесном состоянии R = ![]() . Точные
значения связи 0.195
. Точные
значения связи 0.195 ![]() (2,65 эВ) и R =
(2,65 эВ) и R = ![]() . В антисимметричном случае атомы
отталкиваются, связи нет.
. В антисимметричном случае атомы
отталкиваются, связи нет.
В молекуле ![]() имеется два электрона, которые
могут находиться на одной орбитали с противоположными спинами. Оценочный подход
дает удвоение энергии связи, т.е. 5,3 эВ по сравнению с 2,65 эВ.
Однако здесь необходимо учитывать дополнительную энергию электростатического
отталкивания электронов, что уменьшает энергию связи до 4,72 эВ.
имеется два электрона, которые
могут находиться на одной орбитали с противоположными спинами. Оценочный подход
дает удвоение энергии связи, т.е. 5,3 эВ по сравнению с 2,65 эВ.
Однако здесь необходимо учитывать дополнительную энергию электростатического
отталкивания электронов, что уменьшает энергию связи до 4,72 эВ.
Применим метод орбиталей для молекулы водорода. Будем обозначать
протоны А и В, а электроны — 1 и 2. Учитывая идентичность
электронов, мы получим следующий набор атомных орбиталей: ![]() , из которых можно построить молекулярные
орбитали
, из которых можно построить молекулярные
орбитали
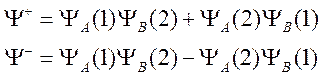 (56)
(56)
соответствующие
симметричному и антисимметричному состояниям. Отражение в вертикальной
(проходящей через ось молекулы) плоскости меняет местами 1 и 2 электроны. При
этом ![]() меняет знак. Оператор Гамильтона для
молекулы может быть представлен в виде
меняет знак. Оператор Гамильтона для
молекулы может быть представлен в виде
![]() ,
,
где
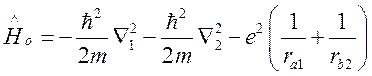 , (57)
, (57)
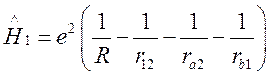 (58)
(58)
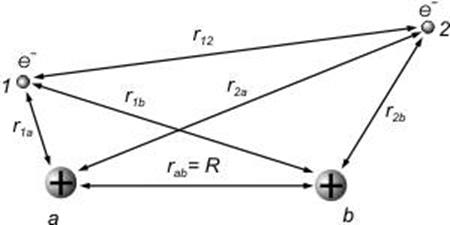
Здесь приняты обозначения, показанные на рис. 14
|

Гамильтониан ![]() (57) описывает невозмущенную
энергию двух атомов. Запись
(57) описывает невозмущенную
энергию двух атомов. Запись ![]() в виде (57)
предполагает
в виде (57)
предполагает ![]() в виде
в виде ![]() . При
вычислении невозмущенной энергии для
. При
вычислении невозмущенной энергии для ![]() в выражении (57) необходимо
поменять местами 1 и 2 электроны.
в выражении (57) необходимо
поменять местами 1 и 2 электроны.
Гамильтониан ![]() (58) описывает энергию
возмущения, которая включает взаимодействие протонов между собой, взаимодействие
электронов между собой и с “чужими” протонами.
(58) описывает энергию
возмущения, которая включает взаимодействие протонов между собой, взаимодействие
электронов между собой и с “чужими” протонами.
Рассматривая энергию взаимодействия ![]() , как
первую поправку к энергии системы, по теории возмущений можно написать
, как
первую поправку к энергии системы, по теории возмущений можно написать
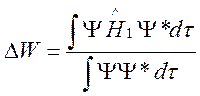 ,
(59)
,
(59)
где
интегрирование производится по всему пространству координат для двух
электронов. Под координатами электронов, как уже отмечалось в (58), необходимо
понимать ![]() ,
, ![]() для
для
![]() и
и ![]() ,
, ![]() для
для ![]() , то
есть в данном случае учитывается взаимодействие электрона и с “чужим” протоном.
, то
есть в данном случае учитывается взаимодействие электрона и с “чужим” протоном.
Введем следующие обозначения
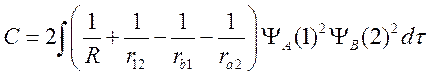 ; (60)
; (60)
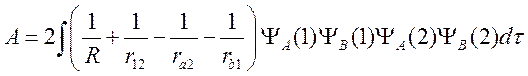 ; (61)
; (61)
![]() ,
(62)
,
(62)
где С —
кулоновский интеграл и ![]() , так как волновые функции
(56) действительные, A — “обменный” интеграл и
, так как волновые функции
(56) действительные, A — “обменный” интеграл и ![]() —
нормировочная добавка. Интерпретация величин С, А,
—
нормировочная добавка. Интерпретация величин С, А, ![]() аналогична интерпретации (20) в теории
атома гелия.
аналогична интерпретации (20) в теории
атома гелия.
С учетом формул (59-62) возмущение энергии можно представить в виде
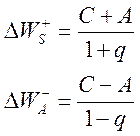 ;
(63)
;
(63)
Как и ожидалось, энергия взаимодействия для симметричных и антисимметричных
функций ![]() различна. Необходимо отметить, что
возмущение
различна. Необходимо отметить, что
возмущение ![]() зависит от расстояния между протонами R,
а полная энергия качественно ведет себя аналогично рис.13 для
зависит от расстояния между протонами R,
а полная энергия качественно ведет себя аналогично рис.13 для ![]() .
.
Действительно, на больших расстояниях между протонами волновые функции
практически не перекрываются, С и А малы. При средних расстояниях
порядка боровского радиуса, перекрытие значительно. Следовательно, обменная
плотность электронного облака велика, локализована между протонами и имеет
минимальное расстояние до ядер, то есть среднее значение ![]() и
и ![]() мало по
сравнению с R и
мало по
сравнению с R и![]() . Таким образом, величина А
отрицательна и по модулю значительно больше C. Поэтому знак
. Таким образом, величина А
отрицательна и по модулю значительно больше C. Поэтому знак ![]() определяется знаком А, т.е. при
средних значениях R ~
определяется знаком А, т.е. при
средних значениях R ~ ![]() величина
величина
![]() отрицательна, а
отрицательна, а ![]() положительна,
следовательно, для симметричной функции получаем притяжение, а для
антисимметричной
положительна,
следовательно, для симметричной функции получаем притяжение, а для
антисимметричной ![]() — отталкивание. При малых расстояниях
определяющую роль начинает играть кулоновское отталкивание ядер.
— отталкивание. При малых расстояниях
определяющую роль начинает играть кулоновское отталкивание ядер.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.