Многоатомные молекулы (Раздел 2.8. учебного пособия)

2.8. Многоатомные молекулы

Проблема многоатомной молекулы очень многогранна, ее изучение должно явиться предметом отдельного курса. Поэтому здесь мы лишь кратко обозначим основные особенности, свойства и методы анализа подобных структур.

Классификация термов многоатомных молекул существенно связана, как и у двухатомных молекул, с их симметрией. Применение теории групп позволяет определить степень вырождения состояний и характер их расщепления под влиянием возмущений, установить общие правила отбора, определяющие разрешенные и запрещенные переходы, классифицировать собственные колебания и т.д. Подробно с применением теории групп к анализу многоатомных молекул можно ознакомиться в [1,6,7].

При нахождении полной энергии молекулы используется приближение, в котором движение электронов, колебательное движение ядер и вращательное движение молекулы, как целого, рассматриваются отдельно. Подобный подход был использован при анализе двухатомных молекул (см. разделы 2.5, 2.6).

В неподвижной системе координат  оператор Гамильтона молекулы состоящей из n электронов и N ядер с зарядами , может быть записан в виде . Здесь:

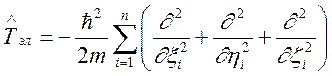;                                (91)

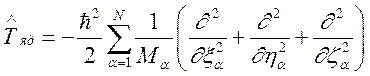;                           (92)

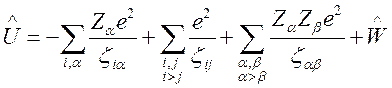,                         (93)

где  — координаты электронов;  — координаты ядер массой ;  — расстояния между электронами и ядрами, между i и j электронами и между - и-ядрами.  - оператор, учитывающий все малые взаимодействия, в частности, связанные со спином электрона.

Оператор  зависит от 3n координат электронов и 3N координат ядер.

Переход в систему центра масс, являясь линейным преобразованием, не меняет вида операторов , при замене координат  на относительные координаты  и . Однако, число независимых координат уменьшается на 3. Учитывая, что положение центра масс практически определяется тяжелыми ядрами, 3N координат будут связаны дополнительными соотношениями:

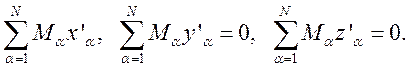
Полученный оператор  включает как кинетическую энергию колебаний, так и кинетическую энергию вращений, а электронное движение в  отнесено к координатной системе, хотя и связанной с центром масс, но оси которой сохраняют неподвижное положение в пространстве.

Следующий шаг состоит в разделении колебаний и вращения, а также в описании электронного движения в координатной системе, связанной с молекулой. С этой целью мы переходим от координатной системы  с началом в центре масс, у которой оси сохраняют ориентацию в пространстве, к подвижной системе x, y, z с началом также в центре масс, но связанной с осями инерции молекулы. При классическом рассмотрении это означает, что углы, определяющие ориентацию подвижных координат осей, меняются со временем. При квантовомеханическом рассмотрении это означает, что операторы, соответствующие механическим величинам, будут содержать дифференцирование по угловым переменным.

При переходе к подвижной системе координат три (для линейной молекулы две) угловые координаты будут определять положение этой подвижной системы, а остальные (3N - 6) (или 3N - 5) координат будут определять относительное положение ядер в нелинейной или линейной молекулах.

В случае двухатомной молекулы разделение оператора  на все части будет точным. Используя сферические координаты

,                   (94)

получим

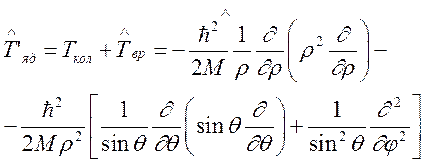,                         (95)

где  — расстояние между ядрами. Первое слагаемое, зависящее от , является оператором кинетической энергии колебаний, а вторые два, зависящие от углов  кинетической энергии вращения.  — момент энерции ядер. Таким образом, уже здесь существует связь колебаний и вращений. При малых амплитудах колебаний можно положить , где  — равновесное расстояние.

В случае многоатомной молекулы разделение оператора  на два оператора  и  может быть проведено только приближенно, если пренебречь членами, определяющими связь колебания и вращения.

                                          (96)

где оператор  кинетической энергии колебаний зависит от 3N - 6 (или 3N - 5) координат, определяющих положение ядер, а оператор  кинетической энергии вращения является квадратичной функцией от операторов проекций моментов количества движения ядер

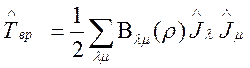,                                      (97)

где индексы ,  пробегают значения x, y, z.

Если оси x, y, z являются главными осями инерции молекулы, то для этой конфигурации выражение (97) принимает вид

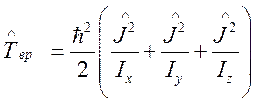,                                  (98)

где ,,  — главные моменты инерции молекулы, как твердого тела.

Таким образом, в подвижной системе координат оператор  может быть записан в виде

,                              (99)

где символы x, ,  обозначают совокупность координат: x — 3n координат электронов;  - 3N - 6 (3N - 5) относительных координат ядер и  — три угловые координаты (2 для линейной молекулы).

Волновая функция

.                            (100)

В соответствии с порядками величин электронной, колебательной и вращательной энергий  сначала решается задача об электронном движении, затем, используя метод последовательных приближений, находится колебательная энергия и затем вращательная. При этом последовательно находятся ,  и .

Для получения решения для электронов рассмотрим оператор

.                                    (101)

Как было показано в разделе (2.1), одна из возможных собственных функций системы, состоящей из n электронов, в нулевом приближении может быть представлена в виде произведения одноэлектронных собственных функций.

,                                    (102)