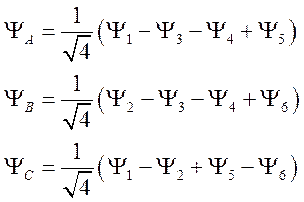Многоатомные молекулы (Раздел 2.8. учебного пособия), страница 3

;                                     (106)

Из (106) видно, что . Это оказывается общим правилом, то есть перекрещивающаяся связь всегда может быть получена, как линейная комбинация двух неперекрещивающихся связей. Эти независимые конфигурации связей без пересечений называются каноническими структурами. Следует отметить, что собственные функции, отвечающие каноническим структурам, образуют полную систему, а их количество равно [6]

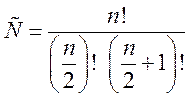,                                         (107)

где n — число валентных электронов.

Возникает вопрос, какая линейная комбинация из этих  функций описывает реальную систему.

.

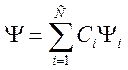Коэффициенты  должны быть найдены вариационным методом из условия минимума энергии системы. Предполагается, что  образуют полную систему функций. Тогда энергия находится из выражения

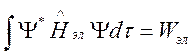.                                 (108)

Основной недостаток метода локализованных электронных пар, рассмотренного кратко выше, состоит в том, что благодаря непреодолимым математическим трудностям приходится пренебрегать взаимной неортогональностью собственных функций.

Существуют и другие способы нахождения собственных функций общей системы; например, основанные на теории самосогласованного поля, метода молекулярных орбит, применение теории групп и т.п. Подробно данные вопросы разобраны в [6].

Решение уравнения

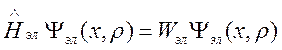                               (109)

позволяет найти электронную энергию , как функцию относительных координат  ядер, то есть ядра предполагались неподвижными.

Решение основного уравнения теории молекул (109) позволяет найти равновесные значения  расстояний между ядрами.

Для нахождения волновых функций, описывающих  колебания и вращения, необходимо усреднить  по электронному движению

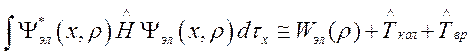.                   (110)

Электронная волновая функция слабо зависит от . Это позволяет при вычислении (110) предположить, что  коммутирует с  и .

Для устойчивых молекул, рассмотрением которых мы пока ограничимся, электронную энергию можно записать в виде

,                                     (111)

где  — значение электронной энергии для равновесной конфигурации и  — дополнительная энергия молекулы, возникающая при смещении атомов из положения равновесия: . Фактически,  является потенциальной энергией колебаний молекулы:

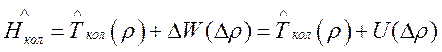                         (112)

и

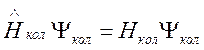.                                         (113)

Рассматривая малые смещения относительно положения равновесия (112) колебательный гамильтониан можно представить в виде:

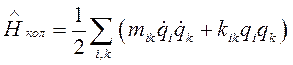,                                  (114)

где суммирование проводится по всем колебательным координатам.

Из механики известно [8], что выбором нормальных координат выражение (114) можно представить в виде

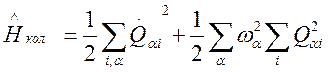,                                (115)

где  — частота нормальных колебаний, i — номер координаты, относящийся к данной частоте. Здесь использована нормировка нормальных координат, позволяющая обратить коэффициенты в  в единицу.

При квантовомеханическом рассмотрении вместо  в (115) должен быть использован оператор импульсов

.

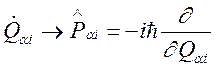Поскольку гамильтониан распадается на сумму N независимых слагаемых вида: 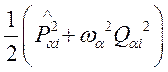, то есть гармонических осцилляторов, то уровни энергии представляются суммами

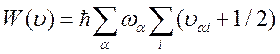,                            (116)

где  — колебательное квантовое число.

Таким образом, каждое нормальное колебание осуществляется независимо и одновременно, и в своей совокупности представляет любое сложное внутреннее движение молекулы.