Многоатомные молекулы (Раздел 2.8. учебного пособия), страница 2

где буквы a, b... - обозначают набор квантовых чисел n, , , , которые имеет электрон, например, в атоме а, а цифры в скобках являются номерами электронов. Учитывая тождественность электронов, а также тот факт, что полная собственная функция многоэлектронной системы должна быть антисимметрична по отношению к перестановке любой пары электронов, из (102) можно построить линейную комбинацию этих функций, которая может быть выражена в виде определителя

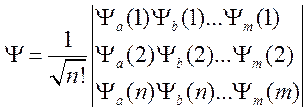.                              (103)

Здесь  — нормировочный множитель. Однако, принимая во внимание, что собственные волновые функции электронов от разных атомов в молекуле не ортогональны, подобная нормировка имеет приближенный характер. Учитывая, что проекция спина  имеет два значения 1/2, можно построить  определителей (число перестановок), подобных (103), которые будут соответствовать одному и тому же значению энергии, но будут отличаться распределением  между электронами. Полная волновая функция будет представлять собой линейную комбинацию из  собственных функций типа (103).

Однако, задача может быть упрощена, если учесть, что устойчивые связи формируются двумя электронами с противоположными проекциями спинов, то есть при n — четном полный спин равен нулю и при n — нечетном S = 1/2. Например, при n = 4 полное число начальных антисимметричных функций типа (103) равно , однако максимальное число связей по два электрона равно 2. Количество возможных конфигураций, образующих эти связи, равно трем

                               a ¾ b       a  b          a  b

                                                  ½        ½             ´                                         (104)

                               c  ¾ d        c d          c d

                                    A              B                   C

Количество же способов размещения проекции спина  между связывающими электронами в этих трех конфигурациях А, В, С будет только шесть

                                               a         b          c         d

                                       +1/2    -1/2    +1/2     -1/2

                                       +1/2     +1/2    -1/2    -1/2

                                       +1/2    -1/2     -1/2    +1/2                               (105)

                                        -1/2    +1/2    +1/2    -1/2

                                        -1/2    +1/2    -1/2    +1/2

                                       -1/2    -1/2    +1/2    +1/2

В этой таблице каждая собственная функция  представляет собой полную антисимметричную функцию (103) с определенным размещением спиновых функций (показаны значения проекций ) между орбиталями a, b, c, d. При этом учтено, что полный спин S равен нулю.

Однако сравнение возможных функций (105) с типами связи (104) показывает, что не каждая функция (105) может образовывать конкретную конфигурацию (104).

Так к конфигурации А относятся четыре функции , , , ;  и . Критерием выбора является равенство нулю спина в каждой связи.

При построении полной функции ,  и  необходимо учесть следующее. Устойчивая связь возникает как мы показывали ранее, когда орбитальная функция симметрична относительно перестановки двух любых электронов. Поскольку полная функция  должна быть антисимметрична, то этим свойством должна обладать спиновая функция, то есть при любой перестановке электронов с их проекциями полная функция меняет знак. Если при образовании  принять, например,  с положительным знаком, то  и  получаются из , в результате одной, то есть нечетной, транспозиции , поэтому они в  должны входить с отрицательным знаком, тогда как  получатся из  в результате двух, то есть четного числа, транспозиций и входят в  со знаком плюс. Следовательно, с учетом указанного свойства имеем: