Ф/Фо=1,88 ехр (0,07t)—0,88 ехр (—3,4t)
Рисунок 1.2 Изменение плотности потока нейтронов во времени при скачкообразном введении положительной реактивности (р==0,003, /==10~3 с)
На рис. 1.2 сплошной линией показано изменение отношения Ф/Фо по (1.55), а штриховыми линиями — изменение каждого члена правой части (1.55) в отдельности. Кривая 1 соответствует изменению первого члена, а кривая 2 — второго. Из рисунка видно, что второй член очень быстро убывает и через 1 с вклад его становится пренебрежимо малым. Поэтому по истечении этого времени изменение плотности потока нейтронов практически определяется первым членом и можно записать
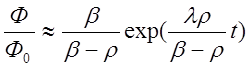(2.56) 1.56
Из последнего выражения следует, что установившийся период реактора
Ty=(b-r)/lr (2.57) 1.57
Если подставить значения в (1.57) b, l и r, которые использовались ранее, то получим
Ty = (0,0064—0,003) / (0,077 • 0,003) ==14,7 с
Установившийся период реактора с учетом запаздывающих нейтронов 14,7 с. Таким образом, переходный процесс будет идти значительно медленней, чем (как показано для тех же условий в § 2 2) без учета запаздывающих нейтронов.
При очень малых значениях
реактивности (примерно 0,01%) в (1.57) значением , r по сравнению с b можно пренебречь, и установившийся период
реактора будет обратно пропорционален реактивности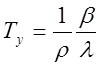 
. Величина 
представляет собой средневзвешенное
время жизни запаздывающих нейтронов 1з.н, т. е. Ту=lзн/r..
Заметим, что это выражение аналогично формуле (1.5), только вместо времени жизни мгновенных нейтронов здесь фигурирует время жизни запаздывающих нейтронов. Поэтому установившийся период реактора полностью определяется свойствами запаздывающих нейтронов.
Период реактора является очень важной эксплуатационной характеристикой и постоянно контролируется в процессе работы, в особенности во время пуска реактора. Величина w, обратная периоду реактора, представляет собой скорость разгона. Чем больше период, тем меньше скорость разгона, и наоборот, с уменьшением периода реактора скорость разгона возрастает.
При больших значениях реактивности период реактора мал и скорость разгона может оказаться настолько большой, что управление реактором будет невозможно. Если r>b, запаздывающие нейтроны практически не оказывают влияния на переходный процесс.
Вводится понятие так называемой мгновенной критичности, которая соответствует состоянию r=b. Это значит, что реактор критичен только на мгновенных нейтронах. А так как кроме мгновенных генерируются и запаздывающие нейтроны, реактор в целом надкритичен с положительной реактивностью r=b и разгон его идет очень быстро с периодом, определяемым мгновенными нейтронами. Таким образом, положительное значение r всегда должно быть меньше b.
При положительном скачкообразном изменении реактивности и r<b плотность потока нейтронов в первый момент времени после внесения возмущения быстро возрастает, а затем постепенно изменяется со скоростью, соответствующей установившемуся периоду реактора. Такой характер изменения плотности потока определяется тем, что мгновенные нейтроны реагируют на скачкообразное изменение реактивности за очень короткий промежуток времени. Однако при r<b дальнейшее быстрое возрастание потока прекращается, так как реактор подкритичен только на одних мгновенных нейтронах, и последующее более плавное изменение плотности потока обусловлено запаздывающими нейтронами.
Легко показать, что изменение плотности потока нейтронов в первый момент времени после внесения возмущения обусловлено мгновенными нейтронами. Для этого выражение (1.54) продифференцируем по времени и возьмем производную в момент t=0
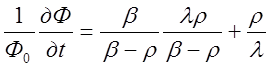
В полученном выражении левая часть представляет собой обратную величину периода, т.е.
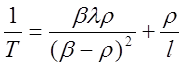
При небольших значениях l первый член в правой части полученного выражения мал по сравнению со вторым и им можно пренебречь. В этом случае
T~l/r~l/Dk.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.