Допустим, что в реакторе, находящемся в критическом состоянии, в некоторый момент времени t скачком происходит малое изменение реактивности, после чего коэффициент размножения сохраняет постоянное значение. Если возмущение достаточно мало, то переходный процесс будет проходить вблизи критического состояния. В этом случае можно считать, что пространственное распределение плотности потока нейтронов не изменяется и описывается основным решением волнового уравнения:
Ñ2Фr+B2Фr=0 (2.19) 1.19
Отсюда
Ñ2Фr= В2Фr (2.20)1.20
Можно показать, что переменные в уравнении (1.17) разделяются. Положим
Ф(r,t)=Фr Фt (2.21)1.21
ci(r,t)=cr,i ct, (2.22)1.22
где Фr и cr,i зависят только от координат, а Фt и ct,i только от времени.
Подставив эти величины в (1.14) и разделив все члены на Ci,r, получим
В (1.22) член Фr/ cr,i не зависит от координат, так как cr,i пропорционально Фr. В этом случае все члены уравнения являются функциями только времени.
Аналогично сделав подстановку в (1.16), разделив все его члены на (1.22) и учтя (1.19), получим:
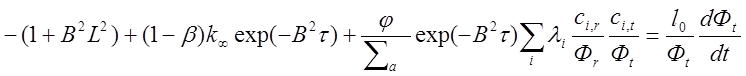(2.24)1.23
Поскольку cr,i/ Фr не зависит от координат, переменные разделяются. Выражения (1.22) и (1.23) — линейные дифференциальные уравнения первого порядка. Решение их ищем в виде
Ф(t)=Aexp(wt) (2.25)1.24
Ci(t)=Ciexp(wt) (2.26)1.25
Необходимо определить, при каких значениях параметраw, имеющего размерность обратного периода, указанные решения удовлетворяют соответствующим уравнениям. Подставим (1.25) и (1.26) в (1.23):
.
Из этого выражения, сокращая на exp(o)Q, получаем
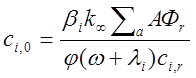(2.27) 1.26
Подставив также (1.25)—(1.27) в (1.24) и сделав элементарные преобразования, найдем
.
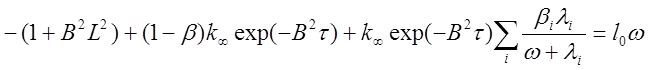Разделив обе части уравнения на 1+L2 B2 , получим
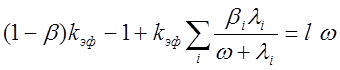(2.28) 1.27
где кэф=кµexp(B2t)/(1+B2L2)—эффективный коэффициент размножения;
l=l0/(1+B2L2)время жизни нейтронов с учетом утечки нейтронов в тепловой области.
По определению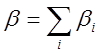 
и кэф1=Dк. Тогда выражение (2.28) можно записать
так:
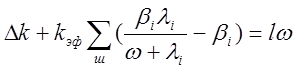(2.29)1.28
После элементарных преобразований
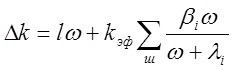(2.30) 1.29
Запишем уравнение (2.30) через реактивность. Для этого разделим все члены на kэф:
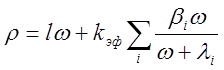(2.31)1.30
Исключив из (2.31) kэф и имея в виду, что r=( kэф1)/ kэф=11/ kэф и 1/ kэф=1r, получим
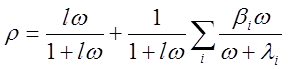(2.32)1.31
Это соотношение является алгебраическим уравнением седьмого порядка относительно w и связывает параметр w с реактивностью реактора. Общий вид решения уравнения (2.32) показан на рис. 2 1
Из графиков на рис. 2.1 видно, что при учете шести групп запаздывающих нейтронов каждому р соответствует семь значений w. С увеличением р корни уравнения (2 32) асимптотически приближаются к значениям —l1, —l2, —l3, —l4, —l5, —l6, —1/l. На рис. 2.1 область, выделенная горизонтальными пунктирными линиями, ограничена значениями р==±1. Для расчета кинетики реакторов практически интересна область |р|<<1. Из рисунка видно, что при любом положительном р все корни, кроме wо, отрицательны, и по порядку величины приближаются к соответствующим значениям постоянных распадаl1, l2, •••l6 ядер предшественников, испускающих запаздывающие нейтроны. Отсюда следует, что плотность потока нейтронов может быть представлена в виде суммы экспонент
Ф(t) =Aоехр (wоt) +A1exp(w1t) + A2exp(w2t) + A3exp(w3t) + A4exp(w4t) + A5exp(w5t) + A6exp(w6t),(2.33)1.32
гдеwо, w1…—корни уравнения (1.32); A0,A1...—коэффициенты, определяемые начальными условиями. В уравнении (1.33) при положительном скачке реактивности все члены, кроме первого, содержат экспоненты с отрицательными показателями. Поэтому
|
|
Рисунок 1.1 Зависимость установившегося периода реактора Ty от реактивности р для различных значений l
;по прошествии некоторого промежутка времени (примерно 1/l1) в нем будет играть роль только первый член, а остальные будут стремиться к нулю, и выражение (1.33) примет вид
Ф(t)=Aоехр(wоt). (2.34)1.33
Из определения периода реактора следует, что wо представляет собой обратную величину установившегося периода реактора:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
