Рассмотрим поведение реактора при нарушении нейтронного баланса, не интересуясь причинами, вызывающими изменение реактивности. Анализ проведем в односкоростной диффузионной модели с непрерывным замедлением. Предполагаем, что изменение реактивности возникает в результате возмущений, вводящихся равномерно по всему реактору, что равносильно точечной модели, когда пространственное распределение нейтронов исключается. Рассматриваем гомогенный реактор без отражателя. Тем не менее, общие выводы справедливы для любых реакторов, в том числе и гетерогенных с отражателем.
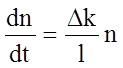1.1
Предположим, что в реакторе имеется n нейтронов в 1 см3. При наличии избыточной реактивности Δk плотность нейтронов n будет увеличиваться. В этом случае прирост числа нейтронов за каждое поколение будет равен n* Δk. Если обозначить теперь l время жизни одного поколения нейтронов, соответствующие периоду от момента рождения его до момента поглощения, то скорость изменения плотности нейтронов будет определяться уравнением
После интегрирования уравнения (1.1) получим:
где n0- число нейтронов в 1 см3 в некоторый начальный момент времени;
n- число нейтронов по прошествии времени t.
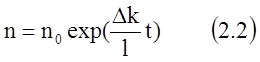1.2
Таким образом, если эффективный коэффициент размножения kэф>1 и имеется положительная избыточная реактивность, то плотность нейтронов растет по экспоненциальному закону. В рамках односкоростной модели связь между плотностью потока и плотностью нейтронов определяется соотношением
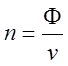(2.3) 1.3
где v- скорость нейтронов , см/с;
Ф- плотность потока нейтронов , нейтрон/(см2 с).
С учетом этого формула (1.2) может быть записана относительно изменения плотности потока нейтронов
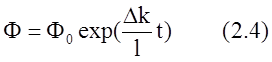1.4
При Δk=0 плотность потока нейтронов Ф=Ф0 и не изменяется во времени. В этом случае реактор находится точно в критическом состоянии. При Δk>0 реактор находится в надкритическом состоянии и плотность потока возрастает. В подкритическом состоянии Δk<0 и плотность потока уменьшается.
Важно отметить, что при определении критического состояния реактора не фигурирует абсолютное значение плотности потока нейтронов. Это означает, что реактор может быть критическим при любом значении плотности потока нейтронов (или на любом уровне мощности).
Период реактора является очень важной характеристикой при рассмотрении кинетики, так как он определяет скорость переходного процесса. Период реактора – это время, в течение которого плотность нейтронов (или мощность реактора) изменяется в е раз. Если Т – период реактора, то согласно определению легко получить, что
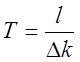(2.5)1.5
Подставив выражение (1.5) в (1.2) , получим
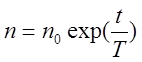(2.6)1.6
В практике эксплуатации для оценки скорости переходного процесса нередко пользуются временем удвоения, т.е. временем, в течение которого мощность реактора изменяется вдвое. Связь между временем удвоения и периодом реактора легко получить из (1.6). Мощность реактора увеличивается в 2 раза, если n/n0=2, т.е. 2=exp(T2/T), где Т2 – время удвоения. Отсюда
Т2=0,693Т (2.7)1.7
Из выражения (1.5) следует, что период реактора определяется временем жизни одного поколения нейтронов в реакторе и избыточной реактивностью. Для любого конкретного реактора время жизни одного поколения нейтронов практически постоянно и период определяется только значением избыточной реактивности, характеризующей степень отклонения системы от критического состояния. При этом, если Δk уменьшить, то период реактора возрастает, а скорость переходного процесса уменьшится. В стационарном режиме избыточная реактивность Δk=0 , а период реактора, как это следует из (1.5), равен бесконечности.
Время жизни одного поколения нейтронов зависит от типа реактора. При одной и той же избыточной реактивности плотность потока нейтронов будет увеличиваться с большей скоростью в том реакторе, в котором время жизни одного поколения нейтронов меньше.
Под временем жизни нейтронов понимают период с момента их рождения до поглощения. Время от момента захвата нейтрона, вызвавшего деление ядра топлива, до появления мгновенных нейтронов деления составляет примерно 10-14-10-15 с. Как уже отмечалось, средняя энергия нейтронов деления около 2 МэВ. В зависимости от типа замедлителя время замедления равно примерно 10-4-10-5 с. Замедлившиеся до тепловых энергий нейтроны диффундируют в реакторе до момента поглощения. Время диффузии тепловых нейтронов составляет 5*10-3-10-4 с. В графитовых реакторах оно равно примерно 10-3 с, в тяжеловодных примерно 5*10-3 с, в реакторах с обычной водой примерно 10-4 с. Таким образом, общее время жизни одного поколения нейтронов определяется временем диффузии и для тепловых реакторов равно 5*10-3-10-4 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
