![]()
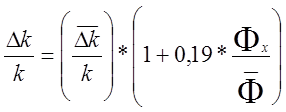 .
(12.1.10)(2.28)
.
(12.1.10)(2.28)
Таким образом,
учет неравномерности плотности нейтронного потока по реактору увеличивает
эффект отравления по сравнению с вычисленным по средней плотности потока.
Физическая причина этого состоит в том , отравление максимально в центре
реактора, где ценность нейтронов наибольшая. Поскольку Фх‹‹![]() , различие между
, различие между ![]() и
и
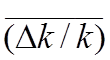 невелико. Например , если
невелико. Например , если ![]() =5*1013 нейтр/(см2*с),
то из (12.1.10) получим (
=5*1013 нейтр/(см2*с),
то из (12.1.10) получим (![]() )=1,03*
)=1,03* 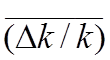 .
.
Если в реакторе имеется один делящийся нуклид, например 235u, то удобно ввести величину qfx:
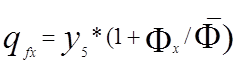 -1.
(12.1.11)(2.29)
-1.
(12.1.11)(2.29)
Коэффициент размножения можно записать так:
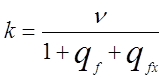 ,
(12.1.12)(2.30)
,
(12.1.12)(2.30)
где ![]() ;
;
![]() - полное макроскопическое сечение радиационного
поглощения (кроме 135Хе ). Тогда изменение коэффициента размножения
при появлении ксенона равно
- полное макроскопическое сечение радиационного
поглощения (кроме 135Хе ). Тогда изменение коэффициента размножения
при появлении ксенона равно
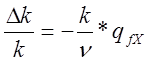 (12.1.13)(2.31)
(12.1.13)(2.31)
Стационарное
отравление 105Rh может быть вычислено по аналогичным формулам, если
заменить ![]() и
и ![]() .
Характерное значение плотности потока нейтронов для 105Rh равно
.
Характерное значение плотности потока нейтронов для 105Rh равно
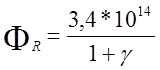 нейтр/(см2*с)
(12.1.14)(2.32)
нейтр/(см2*с)
(12.1.14)(2.32)
где γ — жесткость
спектра. обычно γ≤0.5 ![]() и поэтому
и поэтому![]() ≥2.3*1014
нейтр/(см2*с), что примерно в
30 раз больше, чем
≥2.3*1014
нейтр/(см2*с), что примерно в
30 раз больше, чем ![]() (12.1.5). Поэтому для реакторов
с не очень большой плотностью потока qfX существенно меньше
, что еще уменьшает qfR по
сравнению с qfX .
(12.1.5). Поэтому для реакторов
с не очень большой плотностью потока qfX существенно меньше
, что еще уменьшает qfR по
сравнению с qfX .
Если учитывать неравномерность плотности нейтронного потока по объему реактора , то надо пользоваться формулой (12.1.7). При этом чаще всего осуществляется неравенство Ф(Г)‹‹ФR. В этом случае имеем
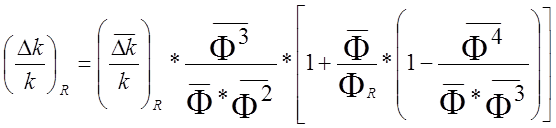 ,
(12.1.15)(2.33)
,
(12.1.15)(2.33)
где 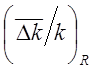 вычислено
для средней плотности потока . Аналогичной формулой надо пользоваться и для
ксенона в тех случаях , когда
вычислено
для средней плотности потока . Аналогичной формулой надо пользоваться и для
ксенона в тех случаях , когда ![]() ‹‹
‹‹![]() . Если Ф(Г)=cosα*z, то
. Если Ф(Г)=cosα*z, то
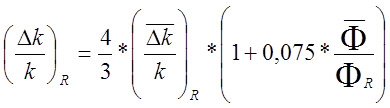 ,
(12.1.16)(2.34)
,
(12.1.16)(2.34)
т.е. ![]() отличается
от
отличается
от 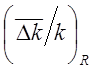 уже в нулевом порядке по малому параметру
уже в нулевом порядке по малому параметру 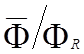 , а коэффициент при члене первого порядка
весьма мал . Поэтому можно ограничиться одним слагаемым в (12.1.15)(2.15), (12.1.16)(2.34). В
большинстве случаев хорошая точность получается , если в (12.1.15) положить
, а коэффициент при члене первого порядка
весьма мал . Поэтому можно ограничиться одним слагаемым в (12.1.15)(2.15), (12.1.16)(2.34). В
большинстве случаев хорошая точность получается , если в (12.1.15) положить
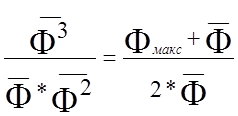 , (12.1.17)(2.35)
, (12.1.17)(2.35)
Например , если Ф(z)= cosα*z, то (12.1.17)(2.35) равно 1,285 вместо точного значения 4/3.
Обратимся
теперь к переходным процессам, который описываются уравнениями (12.1.1)(2.1). Решение
этих уравнений, если плотность потока и ![]() постоянны
во времени, при произвольных начальных условиях I(0), X(0) имеет
следующий вид:
постоянны
во времени, при произвольных начальных условиях I(0), X(0) имеет
следующий вид:
![]() ;
;
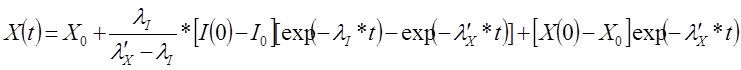 ,( 12.1.18)(2.36)
,( 12.1.18)(2.36)
где I0, X0 определены (12.1.3) (2.3) и
![]() .
(12.1.19)(2.37)
.
(12.1.19)(2.37)
Рис.12.2. Зависимость ![]() от времени при различных плотностях
потоков тепловых нейтронов Ф.
от времени при различных плотностях
потоков тепловых нейтронов Ф.
Если
в (12.1.18)(2.18) положить I(0)= X(0)= 0, то получим закон
увеличения концентраций I и Хе при пуске реактора в момент t=0 , причем плотность потока нейтронов изменяется
скачком от Ф=0 при t‹0 до Ф при t›0. Зная концентрацию Хе , можно
определить макроскопическое сечение и величину qfX как
функцию времени. На рис.12.2 приведена зависимость
![]() для различных плотностей потоков . Если пренебречь
независимым выходом Хе , то I0/X0=
для различных плотностей потоков . Если пренебречь
независимым выходом Хе , то I0/X0=![]() и значение уj
исчезает из отношения
и значение уj
исчезает из отношения ![]() , т.е. это отношение одинаково для
всех делящихся нуклидов.
, т.е. это отношение одинаково для
всех делящихся нуклидов.
При
малых временах, когда ![]() ‹‹1,
‹‹1, ![]() ‹‹1,
можно (12.1.18) разложить в ряд:
‹‹1,
можно (12.1.18) разложить в ряд:
![]()
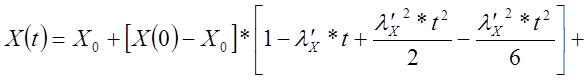
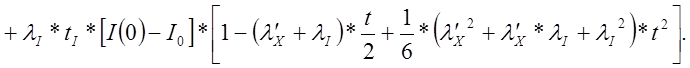 (12.1.20)(2.38)
(12.1.20)(2.38)
При Х(0)=I(0)=0, т.е. для пуска реактора, получим
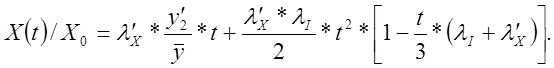 (12.1.21)(2.39)
(12.1.21)(2.39)
Рассмотрим теперь поведение Х(t) при остановке реактора , который долго работал на постоянной мощности. Для этого надо найти решение уравнений (12.1.1)(2.1) при Ф=0 с начальными условиями I(0)=I0, X(0)=X0, где I0 , X0 –концентрации иода и ксенона при t‹0. Это решение получится из (12.1.18) (2.18), если там положить Ф= I0= X0=0 и заменить I(0). X(0) на I0 , X0, т.е.
![]()
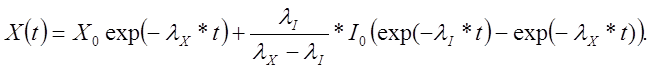 (12.1.22)(2.40)
(12.1.22)(2.40)
Определим отношение qfX(t)/qfX(0), т.е. отношение отрицательной реактивности, вносимой 135Хе после остановки реактора, к стационарному значению qfX до остановки:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.