Кинетика ядерного реактора. Физические процессы, сопровождающие работу ядерного реактора, страница 11

Рис. 12.1. Сечение поглощения ¹³⁵Хе s(Е); среднее сечение по максвелловскому распределению`s(Е_т) и g(Е_т) – фактор (´ – сечение для скорости нейтронов 2200м/с)

Схема образования ¹³⁵Хе выглядит следующим образом (числа под стрелками – периоды полураспада Т_1/2):

 

у1                  у2 IXe,                                 6,61ч        9,083ч

Обычно можно не учитывать коротко живущих предшественников йода, продуктов распада ¹³⁵Хе, изотопа ¹³⁶Хе, который возникает при захвате нейтрона ¹³⁵Хе и Хе^m в метастабильном состоянии (при некоторых переходных процессах пренебрежение Хе^m можно привести погрешности около 5%). Тогда схема распада упрощается (изменение Т_1/2 для йода приближенно учитывает наличие Хе^m):

 

где, у₁ – кумулятивный выход йода, а у₂ – независимый выход ксенона. Значение у₁+у₂=у и у₂/у приведены в таблице 12.1.

Система уравнений, описывающая образование и уничтожение йода и ксенона, имеет следующий вид:

                                    ;                                                                 

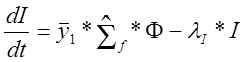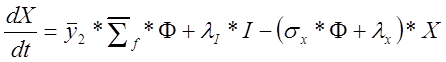.                (12.1.1) (2.19)

где I, Х –числа ядер ¹³⁵ I и ¹³⁵ Хе; l_I, l_х – постоянные распада (l_I =2,895*10^-5 с^-1=0,1042 ч^-1, l_х=2,12*10^-5 с^-1=0,0763 ч^-1); ¯у₁—средний выход йода; ¯у₂ – средний выход ксенона, т.е.

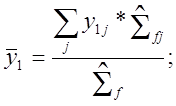
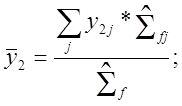                                         (12.1.2)(2.20)

у_1.2j – выходы при деление нуклида j;–макроскопическое сечение деления;–суммарное макроскопическое сечение деления. Резонансный интеграл ¹³⁵Хе можно не учитывать, и поэтому σ_х – сечение в тепловой группе; Φ –  плотность потока тепловых нейтронов .

когда             =0 . Из уравнений (12.1.1) (2.1) получим стационарные кон-

Прежде всего рассмотрим стационарное состояние реактора,

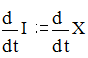центрации I  и Хе:

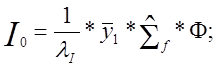
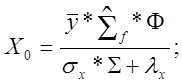
                         .        (12.1.3)(2.21)

Из (12.1.3) имеем макроскопическое сечение Хе:

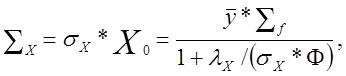                                                (12.1.4)(2.22)

т.е. при достаточно большой плотности потока макроскопическое сечение Хе не зависит от его микроскопического сечения. В этом случае каждое ядро Хе погибает не в результате распада, а в результате захвата нейтрона (получающийся изотоп ¹³⁵Хе стабилен и имеет малое сечение захвата: σ(¹³⁵Хе) = 0,16(3)). Характерное значение плотности потока, когда знаменатель в (12.1.4) (2.22)равен двум,  следующее:

Ф_х = λ_х/σ_х= 0,8*10¹³ нейтр/(см²*с).               (12.1.5)     (2.23)

При этом использовано значение σ_х при скорости 2200м/с; фактически же Ф_х определяется средним значением сечения в тепловой группе и зависит от эффективной температуры нейтронов. Из рис. 12.1 видно, что эта зависимость не очень сильная; при больших плотностях потока (Ф≥ 10¹⁴ нейтр/(см²*с)) ее можно не учитывать, поскольку Σ_х уже почти не зависит от σ_х.

Изменение реактивности, вызванное накоплением ксенона, равно

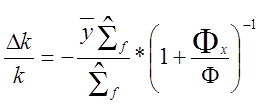                        ,                                   (12.1.6) (2.24)

где—полное макроскопическое сечение поглощения, и предполагается, что плотность потока нейтронов не зависит от координат. Фактически конечно, такая зависимость существует. Пользуясь теорией возмущений получаем

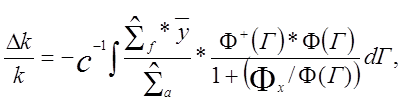                                            (12.1.7)(2.25)

где

                                           

Если плотность  потока нейтронов столь велика, что Ф_х/Ф(г) << 1, то в (12.1.7) можно провести разложение в ряд. Тогда, предполагая, что  не зависит от координат и что Ф⁺=Ф, находим

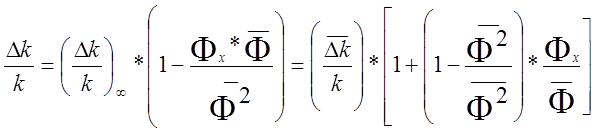 ,(12.1.8)            (2.26)

где (Δk/k)_∞ -- изменение реактивности при бесконечно большой плотности потока, а 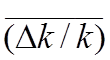 --изменение реактивности, вычисленное для средней  плотности потока, т.е.

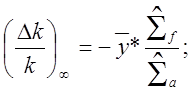
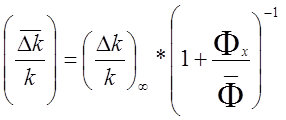    .       (12.1.9)(2.27)

Пусть, например , коэффициент выравнивания по радиусу равен 1, а распределение плотности потока по высоте дается зависимостью Ф(z) =cosα*z. Тогда ()²=0,405, ²=0,5 и