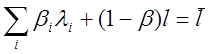Кинетика ядерного реактора. Физические процессы, сопровождающие работу ядерного реактора, страница 3

(2.9)1.9

Таблица 1.3. Выход запаздывающих нейтронов при делении ядер тепловыми и быстрыми нейтронами

Делящий нуклид	Суммарная доля запазды­вающих нейтронов р		Делящий нуклид	Суммарная доля запазды­вающих нейтронов р
	Делений на тепловых нейтронах	Деление на быстрых нейтронах		Деление на тепловых нейтронах	Деление на быстрых нейтронах
23&U 239рц 233 \J	0,0064 0,0021 0,0026	0,0060 0,0020 0,0026	238Ц 232Th	—	0,0155 0,0190

В правой части выражения (1.9) второй член мал по сравне­нию с первым, поэтому время жизни одного поколения нейтронов определяется запаздывающими нейтронами: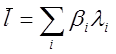

Нужно отметить, что средняя энергия, при которой генерируются запаздывающие нейтроны, около 0,5 МэВ, а мгновенных нейтронов около 2 МэВ. Это обстоятельство приводит к повышению процентного содержания их, что особенно заметно в небольших реакторах, где утечка нейтронов велика.

В табл. 1.3 приводятся данные по суммарному выходу запаздывающих нейтронов при делении ядер тепловыми и быстрыми нейтронами.

Из приведенной таблицы следует, что в реакторах на быстрых и тепловых нейтронах доля запаздывающих нейтронов для деля­щихся нуклидов остается практически одинаковой. А если учесть, что быстрыми нейтронами делятся и воспроизводящие материалы, то эффективная доля запаздывающих нейтронов возрастает.

1.4  Кинетика реакторов с учетом запаздывающих нейтронов

Односкоростное нестационарное уравнение диффузии имеет следующий вид:

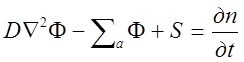(2.10)                                              (1.10)

где первый член в левой части характеризует диффузию, второй — поглощение и третий—генерацию нейтронов. Правая часть уравнения представляет собой изменение плотности нейтронов во времени. В уравнении (1.10) дополнительные обозначения следующие: D—коэффициент диффузии нейтронов, см; S_а—макроскопическое сечение поглощения, см¹; S—плотность источников нейтронов, нейтр/(см³ с).

Поскольку происходит генерация мгновенных и запаздывающих нейтронов , в (1.10) источники можно представить в виде суммы

 (2.11)1.11

где S₁—источники от мгновенных нейтронов; S₂—источники от запаздывающих нейтронов.

Согласно теории возраста генерация мгновенных нейтронов деления описывается выражением

k_¥S_aФexp(B²t)(2.12)1.12

где k_¥S_aФ —количество нейтронов, возникающих в процессе деления в единице объема в единицу времени; exp(B²t) учитывает утечку нейтронов в процессе замедления; В² — материальный параметр, см²; t—квадрат длины замедления, см².

С учетом генерации запаздывающих нейтронов источники от мгновенных нейтронов деления определяются формулой

S₁=(1b)k_¥S_aФexp(B²t) (2.13)1.13

гдеb—доля запаздывающих нейтронов.

Для определения источников от генерации запаздывающих нейтронов составим вначале уравнение, описывающее изменение концентрации ядер предшественников, испускающих запаздывающие нейтроны. Предположим, что ядра предшественники образуются непосредственно при делении. Тогда скорость образования 1х ядер, испускающих запаздывающие нейтроны в предшествующем поколении, будет равна

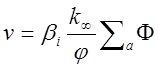(2.14)1.14

гдеb—вероятность избежать резонансного поглощения нейтронов в процессе замедления.

Если обозначить c_i концентрацию предшественников запаздывающих нейтронов 1й группы, то l_ic_i будет характеризовать их убыль вследствие радиоактивного распада. Таким образом, скорость изменения концентрации ядер, излучающих запаздывающие нейтроны iv. группы, запишется в виде

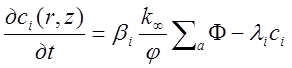 (2.15)1.15

Генерация запаздывающих нейтронов всех групп равна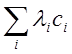

Умножив эту величину на j и на ехр(—В²t), получим выражение для источников от запаздывающих нейтронов

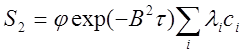 (2.16)1.16

С учетом выражений (1.12) и (1.13), а также соотношения (1.3) уравнение (1.11) запишется в следующем виде:

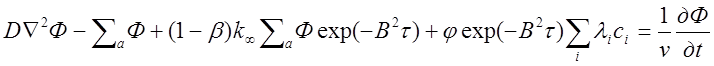 (2.17)1.17

Разделив обе части уравнения наS_a и сгруппировав второй и третий члены в левой части уравнения, получим

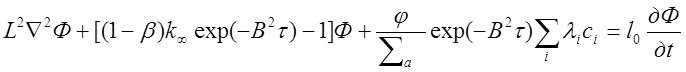(2.18)1.18

где L²=D/S_a квадрат длины диффузии тепловых нейтронов;

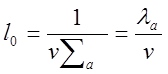время жизни мгновенных нейтронов в бесконечной среде(l_a—средняя длина свободного пробега нейтронов от момента рождения до момента поглощения).