wо =1/Ty (2.35)1.34
где Ty —установившийся период реактора.
Подставив в уравнение (1.31) вместо w установившийся период реактора, получим
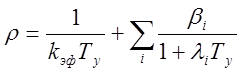 (2.36)1.35
(2.36)1.35
Если предположить, что реактивность р весьма мала (р<<b), то установившийся период Ty велик и в знаменателе под знаком суммы в уравнении (1.36) можно пренебречь единицей по сравнению с произведением liTy. При р весьма малом, kэф близок к единице, и можно записать
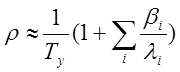 (2.37)1.36
(2.37)1.36
Величина 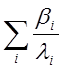 есть среднее время жизни
запаздывающих нейтронов, которое значительно больше, чем время жизни
мгновенных нейтронов l. Тогда, пренебрегая величиной l, получаем
есть среднее время жизни
запаздывающих нейтронов, которое значительно больше, чем время жизни
мгновенных нейтронов l. Тогда, пренебрегая величиной l, получаем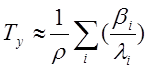
Отсюда следует, что установившийся период реактора при малых значениях р не зависит от времени жизни мгновенных нейтронов и скорость переходного процесса определяется свойствами запаздывающих нейтронов.
При больших значениях р время
жизни мгновенных нейтронов начинает оказывать влияние на установившийся период Ty. Предположим, что р>>b. В этом случае установившийся период
реактора Ty будет настолько мал, что
в (2.36) произведением liТу по сравнению с единицей можно
пренебречь и р~l/kэфТу+b. Отсюда 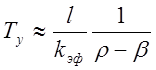 . Пренебрегая величиной b по сравнению с р, получаем
. Пренебрегая величиной b по сравнению с р, получаем 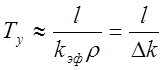 . Это
выражение в точности совпадает с формулой (1.5), в которой период
реактора определяется только временем жизни мгновенных нейтронов.
. Это
выражение в точности совпадает с формулой (1.5), в которой период
реактора определяется только временем жизни мгновенных нейтронов.
Для реактора на тепловых нейтронах, работающего на 235U, зависимость установившегося периода реактора от реактивности при различных значениях l показана на рис. 2.2. Видно, что при малых значениях р величина Tу не зависит от l. При увеличении р начинает сказываться влияние величины l, причем для реакторов с меньшими значениями l уменьшение Tу с ростом р в этой области идет быстрее. Отсюда следует, что при реактивности р<0,005 (b= 0,0064) установившийся период реактора определяется запаздывающими нейтронами независимо от времени жизни мгновенных нейтронов (или, другими словами, независимо от типа реактора, работающего на тепловых нейтронах). При больших значениях реактивности, приближающихся к величине р, скорость переходного процесса велика и зависит от времени жизни мгновенных нейтронов.
Очевидно, что этот вывод справедлив и для реакторов других типов, в частности на быстрых нейтронах. Однако следует помнить, что время жизни мгновенных нейтронов в быстрых реакторах на несколько порядков меньше, чем в реакторах на тепловых нейтронах. В них может быть заметно меньшей и доля запаздывающих нейтронов b, в особенности если в качестве делящегося изотопа используется 239Pu. Поэтому значение избыточной реактивности должно быть еще более ограничено.
Выражение (1.36) обычно называют уравнением «обратных часов», а реактивность р, соответствующую установившемуся периоду Tу=1 ч,—«обратным часом». Если в (1.36) подставить значения величин, которые мы использовали ранее, и Tу положить равным 3600 с, то реактивность, соответствующая одному обратному часу, будет равна примерно 2,Зx10-5. На практике переходные процессы протекают обычно со значительно меньшим периодом, например в течение нескольких десятков секунд, а соответствующая избыточная реактивность приблизительно на два порядка выше. Поэтому понятие «обратные часы» практического использования не получило.
Решение уравнений кинетики с учетом всех групп запаздывающих нейтронов довольно громоздко и выполняется обычно на вычислительных машинах. Для оценочных расчетов переходных процессов можно использовать сравнительно простую модель с учетом одной средневзвешенной группы запаздывающих нейтронов. В этом случае выражение (1.31) принимает вид
r=lw/kэф+bw/(w+l) (2.38)1.37
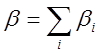 — доля запаздывающих нейтронов;
— доля запаздывающих нейтронов; 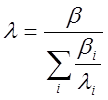 среднее значение постоянной распада
излучателей запаздывающих нейтронов.
среднее значение постоянной распада
излучателей запаздывающих нейтронов.
Ограничимся рассмотрением реактора, работающего на тепловых нейтронах, в котором в качестве делящегося нуклида используется 235U. Тогда суммарная доля запаздывающих нейтронов b=0,0064, а постоянная распада l=0,077 с~'. Для упрощения дальнейших преобразований предположим, что k’эф ~1.Тогда уравнение (1 38) запишется так.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.