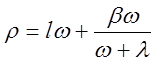(2.39)1.38
Решив его относительноw , получим
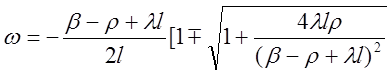(2.40) 1.39
Выражение вида 
при
х<=1 можно разложить в ряд Тейлора
.
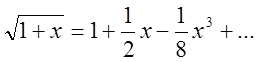В реакторах на тепловых нейтронах время жизни мгновенных нейтронов l не превышает 5 10-3 с Если принять р=0,003, l=0,077, то 4llp=40,077*51О-3 *0,003=4,62 10-6; (b—р+ll)2= (0,0064— 0,003+0,077 •510-3)2 =14,3.10 -6 и 4llp /(b—р+ll)2=4,62 10 –6/14.3*10-6 ~0,3<1.
В графитовых и водо-водяных реакторах, в которых l~10-3 и ~10-4 с соответственно, это соотношение будет значительно меньше единицы. Поэтому, ограничившись в разложении двумя первыми членами, представим выражение (1.40) в виде:
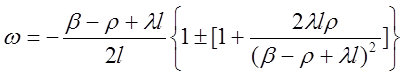
решение которого даетw0=lr/(b-r+ll), w1=-(b-r+ll)/l. Отметим, что при определенииw1 мы пренебрегли членом в квадратных скобках. Если учесть, что ll<<b-r (при r= 0,003, что обычно имеет место при переходных процессах), то произведением ll также можно пренебречь, тогда окончательно получим:
w0=lr/(b-r) (2.41) 1.40
w1=-(b-r+ll)/l.(2.42) 1.41
При положительном скачке реактивности и b-r>0 w0 положительно, a w1 отрицательно.
Выражение (1.33), описывающее изменение плотности потока нейтронов во времени, при одной средневзвешенной группе запаздывающих нейтронов примет вид
Ф(t) ==Aо ехр(w0t) +A1 exp(w1t), (2.43)1.42
а концентрация предшественников запаздывающих нейтронов в соответствии с (2.26) будет выражаться соотношением
с (t) == Соехр (w0t) +C1exp (w1t). (2.44)1.43
Коэффициенты A и С в (1.43) и (1.44) являются постоянными интегрирования и определяются из начальных условий.
С учетом одной группы запаздывающих нейтронов уравнение (1.15) примет вид
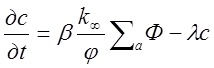(2.45)1.44
Подставляя в (1.45) вместо Ф и С их значения из (1.43) и (1.44),
получаем
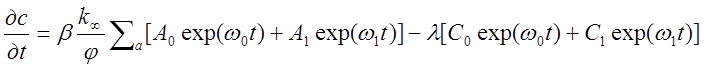(2.45a).1.45
Продифференцируем теперь уравнение (1.44)
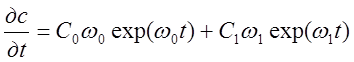(2.456)1.46
Из сравнения последних двух уравнений видно, что правые части их равны, если приравнять соответствующие коэффициенты при одинаковых экспонентах
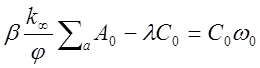
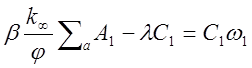
отсюда коэффициенты Со и Ci будут равны:
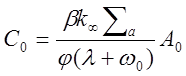
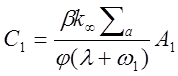
Подставляя в эти выражения вместо w0 иw1 их значения из (1.41) и (1.42) и пренебрегая величинойll, получаем
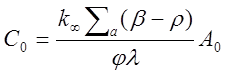(2.46)1.47
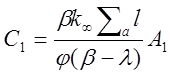(2.47)1.48
Для определения постоянных коэффициентов воспользуемся начальными условиями. В момент времени t=0 в соответствии с (1.43) и (1.44)
Ф=Фо==Aо+A1 (2.48)1.49
c==co+Co+C1, (249)1.50
где Фо и Со — плотность потока нейтронов и концентрация предшественников запаздывающих нейтронов до внесения возмущения соответственно.
В момент времени t=0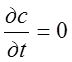 
или согласно (245)
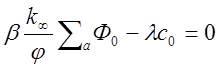(2.50)1.51
Из (2.50) следует, что
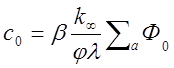(2.51)1.52
Подставив теперь в (1.49) со из (1.51), а вместо Со и C1 выражения из (1.46) и (1.47), будем иметь
.
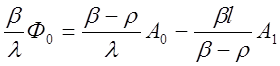Используя (2.48), заменяем в последнем выражении А1 на Фо—Ао. Тогда
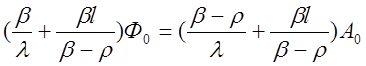
Второй член в скобках правой и левой частей bl/(b-r) при r<=0,5b, характерном для переходных процессов, мал по сравнению с первым, и им можно пренебречь. С учетом этого
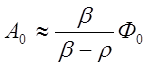(2.52) 1.53
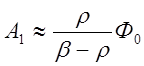(2.53) 1.54
Подставив эти выражения, а также (1.41) и (1.42) в уравнение (1.43), получим формулу для плотности потока нейтронов в зависимости от времени:
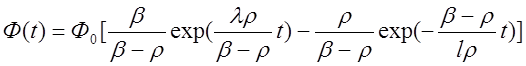(2.54) 1.55
Изменение плотности потока нейтронов определяется алгебраической суммой двух членов. Первый из них отражает вклад запаздывающих нейтронов, так как показатель экспоненты содержит постоянную распада ядер предшественников l, а второй— мгновенных, что видно из показателя экспоненты, содержащей время жизни мгновенных нейтронов l. При t=Q выражение в скобках равно единице и, как следовало ожидать, Ф==Фо.
При r>0 и (b—r)>0 плотность потока нейтронов представляет собой разность двух членов, из которых положительный член растет, а отрицательный быстро убывает.
|
|
Для иллюстрации подставим в (2.54) значения величин. Предположим, как и ранее, l=10-3 с, r=0.003, b=0,0064, l=0,077 c-1, тогда
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
