Розв’язування систем лінійних алгебраїчних рівнянь. Абсолютна величина і норма матриці

Розділ 3

Розв’язування систем лінійних алгебраїчних рівнянь (СЛАР)

Абсолютна величина і норма матриці

Нерівність

                                                                                            (1)

між матрицям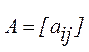и  й  одного типу означає,  що

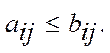                                                                                     (2)

В такому сенсі не всякі дві матриці можна порівняти між собою.

          За абсолютну величину (модуль) матриці  будемо вважати матрицю

де  – модулі елементів матриці .

          Якщо  і  – матриці, для яких операції  і  мають сенс, то:

  а)

  б)

  в) , (  - число).

          Зокрема, одержуємо:, ( - натуральне число).

Під нормою матриці  розуміємо дійсне число

, що задовольняє  умовам:

а) причому  тоді і тільки тоді, коли =0;

б) (  - число ) і, зокрема, ;

в)

г)

( і  - матриці, для яких відповідні операції мають сенс). Зокрема, для квадратної матриці маємо:

де - натуральне число.

          Відзначимо ще одну важливу нерівність між нормами матриць  і  однакового типу. Застосовуючи умову в), будемо мати:

Звідси

Аналогічно

Отже,

          Назвемо норму канонічною, якщо додатково виконані умови:

          д) якщо  то

причому для скалярної матриці  маємо

          е) з нерівності  (А і В – матриці ) випливає нерівність

Зокрема, .

Надалі для матриці   довільного типу ми будемо розглядати головним чином три норми, що легко обчислюються:

          1) 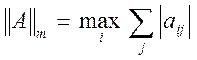   (m – норма);

          2) 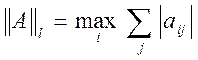    ( - норма);

          3) 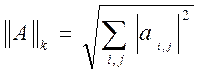 ( - норма).

          Приклад. Нехай

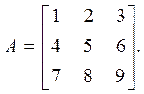
Маємо:

§ 9. Границя матриці

Нехай маємо послідовність матриць

                                                      (1)

одного типу

За границю послідовності матриць  вважається матриця

                                                        (2)

Послідовність матриць, що має границю ,називається збіжною.

Лема 1. Для збіжності послідовності матриць до матриці  (до =1,2,…)до матриці А необхідно і достатньо, щоб

                             при                           (3)

де будь-яка конічна норма матриці А. При цьому

          Доведення. Дійсно, якщо то

  при  

Звідси  де I – одинична матриця розміру .

У силу властивостей норми маємо:

  при  

отже,

          Назад, нехай виконана умова (3). Тоді при  маємо:

і, отже,

тобто

Крім того, якщо  то маємо:

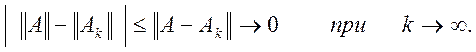
Тому                            

          Висновок: Послідовність  де  тоді і тільки тоді, коли

де  яка-небудь канонічна норма.

          Легко переконатися, що якщо

  і    то:

          a)

          б)

          в)

передбачаючи, що відповідні операції мають сенс. Зокрема, якщо  – матриця така, що можливе множення  і  то

і

          Лема 2. Для збіжності послідовності матриць    необхідно і достатньо, щоб був виконаний узагальнений критерій Коші, а саме: для всякого  повинен існувати такий номер  , що при

, де  - будь-яка канонічна норма.

Алгебраїчна проблема власних значень.

Алгебраїчна проблема власних значень формулюється таким чином: знайти числа  та вектори , , для яких

,                                         (46)

де А – задана матриця з множини Mat_n (C) (n x n) – матриць з комплексними елементами; С – множина комплексних чисел. Числа l називаються власними числами (значеннями), а відповідні вектори х – правими власними векторами матриці А.

          Множина

утворює підпростір векторів простору Cⁿ, і цей підпростір має розмірність

Число є тоді і лише тоді власним числом матриці А, коли L(l)¹0, тобто коли , і

.

Многочлен

називається характеристичним многочленом матриці А, і його корені є власними значеннями А. Якщо l₁, ..., l_k є різними коренями X_A(l), то

Число s(l_і)=s_і називається кратністю власного значення, точніше алгебраїчною кратністю.

          Власні вектори матриці А визначаються неоднозначно: якщо х, у є власними векторами, що відповідають власному значенню , то і є відповідним до  власним вектором. Нуль-вектор разом з власними векторами  якраз і заповнюють підпростір L(l), а його розмірність, тобто максимальне число лінійно-незалежних векторів, що відповідають l, називається геометричною кратністю власного значення l. Відомо, що

.

В силу рівностей

маємо: якщо l₀ є власним значенням матриці А, то l₀ є власним значенням і матриці А^Т, а  є власним значенням А^*. Із співвідношень

випливає, що , але між х та у чи х та z не існує таких простих співвідношень. Вектор z називається спряженим до х.

Оскільки  і , то  називається ще лівим власним вектором матриці А, який відповідає власному значенню l₀. Неважко також помітити , що перетворення подібності

,

де  зберігає власні значення, а відповідні власні вектори х змінює за формулою. Не змінюється при цьому характеристичний поліном, а також числа r(l) та s(l): для s(l) це випливає з інваріантності характеристичного многочлена, а для r(l) – з того, що для вектори х₁, ..., х_r є лінійно незалежними тоді і тільки тоді, коли лінійно незалежними є На еквівалентних перетвореннях ґрунтується багато чисельних методів розв’язування проблем власних значень і власних векторів.