Чисельна апроксимація функцій (Звіт до лабораторної роботи № 5)

Міністерство освіти і науки України

Сумський державний університет

Кафедра комп`ютерних наук

Звіт до лабораторної роботи №5

з предмету «Чисельні методи»

на тему:

«Чисельна апроксимація функцій»

Виконала

Студентка групи ІН-91

Татарченко А.

Перевірила:

Назаренко Л.Д.

Суми 2011

Варіант №10

1.  Умова задачі:

Аналітичний опис результатів 9експериментів, у кожному з яких на вхід системи подається значення параметра Х, а на виході реєструється реакція У.

1 Вибрати вид функції.

2 Методом найменших квадратів знайти коефіцієнти.

10	X	11,2   12,6   18,6   21,4   25   29,6    31,1  38,2   40
	Y	0,99   0,74   0,69   0,58  0,41 0,33  0,26   0,19   0,1

2.  Обґрунтування алгоритму.

                                            y=

                            

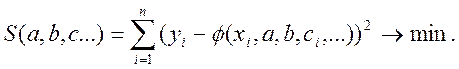
Необхідною умовою екстремуму функції S(a,b,c) є справдження рівностей

                                                  

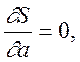
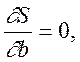
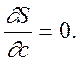
Використовуючи правила диференціювання, рівнянням можна надати вигляд                

          

                                   

        

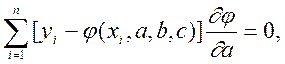
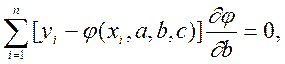
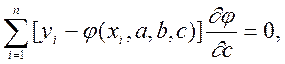
де 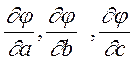-часткові похідні функції y=.

Достатня умова мінімуму функції декількох змінних поля-гає в позитивній визначеності матриці Гессе, складеної з похід-них другого порядку в критичній точці.

У випадку знаходження мінімуму методом найменших квадратів можна не перевіряти матрицю Гессе, тому що функція, яка обмежена знизу , необмежена зверху і має тільки одну підозрі-лу на екстремум точку, може набувати в ній тільки мінімум.

Вибір вигляду регресійної залежності можна здійснити за таблицею. Для цього за вихідними даними обчислюють середні значення х_ср та у_ср :

,  ,  ,

    .

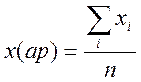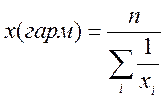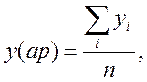
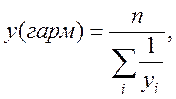
Величина обчислюється так:

1) якщо  збігається з одним із вихідних , то ;

2) якщо  знаходиться між  і ,  знаходимо як ординату відповідної точки на відрізку прямої, що з'єднує вузли  і , за формулою

.

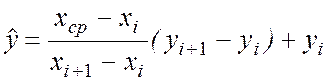Вибір рівняння регресії здійснюється шляхом пошуку міні-мального значення виразу 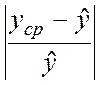 і відповідної йому функції.

Номер п/п					Вигляд функції
1	х(ар)	у(ар)			у=а0+a1x
2	х(геом)	у(ар)			y=a0+a1lnx
3	х(гарм)	у(ар)			у=а0+а1/x
4	х(ар)	у(геом)			y=a0a1x
5	х(геом)	у(геом)			y=a0xa1
6	х(гарм)	у(геом)			y=exp(a0+a1/x)
7	х(ар)	y(гарм)			y=1/(a0+a1x)
8	х(геом)	у(гарм)			y=1/(a0+a1lnx)
9	х(гарм)	у(гарм)			y=x/(a0+a1x)

1. Вибір вигляду функції.

За наведеним вище алгоритмом знаходимо вигляд функції.

Номер п/п					Вигляд функції
1	25,3	0,476667	-1,52786	1,311983793	у=а0+a1x
2	23,237061	0,476667	0,651358	0,26819538	y=a0+a1lnx
3	21,1139068	0,476667	0,591239	0,193783964	у=а0+а1/x
4	25,3	0,298869	0,395833	0,244961945	y=a0a1x
5	23,237061	0,298869	0,44066	0,321768807	y=a0xa1
6	21,1139068	0,298869	0,726018	0,588344421	y=exp(a0+a1/x)
7	25,3	0,387274	0,317183	0,220980455	y=1/(a0+a1x)
8	23,237061	0,387274	0,938147	0,58719222	y=1/(a0+a1lnx)
9	21,1139068	0,387274	0,052785	6,336858462	y=x/(a0+a1x)

З таблиці видно, що найкраще підходить  у=а0+а1/x  функція.

2.Методом найменших квадратів знаходимо коефіцієнти.

Припустимо відомо ,що між x і y існує лінійна залежність y= Невідомі коефіцієнти  знайдемо з необхідної умови екстремуму функції

.                             

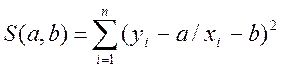У результаті одержимо два рівняння:

                                 

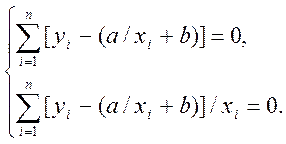
Розв’язуючи систему, знаходимо a і b , що при заданому вигляді рівняння регресії забезпечують мінімум S:

a= ,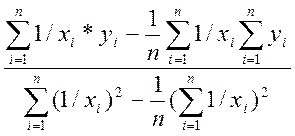

                                                 b=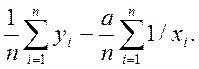

Реалізацію цього методу робимо на мові С.

Програма:

#include<stdio.h>

#include<conio.h>

#include<math.h>

#include<stdlib.h>

#define n 9

#define m 9

int main()

{

 double x[n],y[n],xs[m],ys[m],yk[m],err[m],min,a0,a1;

 int i,k;

 FILE *f;

 clrscr();

 f=fopen("LR5.txt","r");

 if(f==NULL)

 {

  getch();

  return 0;

 }

 for(i=0;i<n;i++)

  fscanf(f,"%lf",&x[i]);

 for(i=0;i<n;i++)