Чисельна апроксимація функцій (Звіт до лабораторної роботи № 5), страница 2

  fscanf(f,"%lf",&y[i]);

 fclose(f);

 xsr(x,xs);

 ysr(y,ys);

 ykr(x,y,xs,yk);

 er(yk,ys,err);

 min=err[0];

 k=1;

 for(i=1;i<m;i++)

  if(err[i]<min)

  {

   min=err[i];

   k=i+1;

  }

 switch(k)

 {

  case 1: f1(x,y,a1,a0); break;

  case 2: f2(x,y,a1,a0); break;

  case 3: f3(x,y,a1,a0); break;

  case 4: f4(x,y,a1,a0); break;

  case 5: f5(x,y,a1,a0); break;

  case 6: f6(x,y,a1,a0); break;

  case 7: f7(x,y,a1,a0); break;

  case 8: f8(x,y,a1,a0); break;

  case 9: f9(x,y,a1,a0); break;

 }

// f1(x,y,a0,a1);

 getch();

 return 1;

}

double zar(double *z)

{

 int i;

 double s;

 s=0;

 for(i=0;i<n;i++)

  s+=z[i];

 return s/n;

}

double zge(double *z)

{

 double p;

 int i;

 p=1;

 for(i=0;i<n;i++)

  p*=*(z+i);

 return pow(p,1.0/n);

}

double zga(double *z)

{

 double pg;

 int i;

 pg=0;

 for(i=0;i<n;i++)

  pg+=1/(*(z+i));

 return n/pg;

}

void xsr(double *x,double *xs)

{

 double xar,xge,xga;

 int i;

 xar=zar(x);

 xge=zge(x);

 xga=zga(x);

 for(i=0;i<m;i+=3)

  *(xs+i)=xar;

 for(i=1;i<m;i+=3)

  *(xs+i)=xge;

 for(i=2;i<m;i+=3)

  *(xs+i)=xga;

}

void ysr(double *y,double *ys)

{

 double yar,yge,yga;

 int i;

 yar=zar(y);

 yge=zge(y);

 yga=zga(y);

 for(i=0;i<3;i++)

  *(ys+i)=yar;

 for(i=3;i<6;i++)

  *(ys+i)=yge;

 for(i=6;i<9;i++)

  *(ys+i)=yga;

}

void ykr(double *x,double *y,double *xs,double *yk)

{

 int i,j;

 for(i=0;i<n;i++)

 {

  if(fabs(xs[i]-x[i])<0.00001)

   yk[i]=y[i];

  else

  {

   for(j=0;j<n-1;j++)

    if( (x[j]<xs[i]) && (x[j+1]>xs[i]))

    {

     yk[i]=(y[j+1]-y[j])/(x[j+1]-x[j])*(xs[i]-x[j])+y[j];

     break;

    }

  }

 }

}

void er(double *yk,double *ys,double *yer)

{

 int i=0;

 for(i=0;i<m;i++)

  yer[i]=fabs((yk[i]-ys[i])/(yk[i]));

}

void f1(double *x,double *y,double &a0,double &a1)

{

 a1=fa1(x,y);

 a0=fa0(x,y,a1);

 printf("y=%.2lf+(%.2lf)x",a0,a1);

}

void f2(double *x,double *y,double &a0,double &a1)

{

 double x1[n];

 int i;

 for(i=0;i<n;i++)

  x1[i]=1.0/x[i];

 a1=fa1(x1,y);

 a0=fa0(x1,y,a1);

  printf("y=%.2lf+(%.2lf)/x",a0,a1);

}

void f3(double *x,double *y,double &a0,double &a1)

{

 double x1[n];

 int i;

 for(i=0;i<n;i++)

  x1[i]=log(x[i]);

 a1=fa1(x1,y);

 a0=fa0(x1,y,a1);

  printf("y=%.2lf+(%.2lf)ln(x)",a0,a1);

}

void f4(double *x,double *y,double &a0,double &a1)

{

 double y1[n];

 int i;

 for(i=0;i<n;i++)

  y1[i]=log(y[i]);

 a1=exp(fa1(x,y1));

 a0=exp(fa0(x,y1,a1));

 printf("y=%.2lf*(%.2lf)^x",a0,a1);

}

void f5(double *x,double *y,double &a0,double &a1)

{

 double x1[n],y1[n];

 int i;

 for(i=0;i<n;i++)

 {

  x1[i]=log(x[i]);

  y1[i]=log(y[i]);

 }

 a1=fa1(x,y1);

 a0=exp(fa0(x,y1,a1));

 printf("y=%.2lf*x^(%.2lf)",a0,a1);

}

void f6(double *x,double *y,double &a0,double &a1)

{

 double x1[n],y1[n];

 int i;

 for(i=0;i<n;i++)

 {

  x1[i]=1.0/x[i];

  y1[i]=log(y[i]);

 }

 a1=fa1(x1,y);

 a0=fa0(x1,y,a1);

 printf("y=exp(%.2lf+(%.2lf)/x)",a0,a1);

}

void f7(double *x,double *y,double &a0,double &a1)

{

 double y1[n];

 int i;

 for(i=0;i<n;i++)

  y1[i]=1.0/y[i];

 a1=fa1(x,y1);

 a0=fa0(x,y1,a1);

 printf("y=1/(%.2lf+(%.2lf)x)",a0,a1);

}

void f8(double *x,double *y,double &a0,double &a1)

{

 double x1[n],y1[n];

 int i;

 for(i=0;i<n;i++)

 {

  x1[i]=log(x[i]);

  y1[i]=1.0/y[i];

 }

 a1=fa1(x1,y1);

 a0=fa0(x1,y1,a1);

 printf("y=1/(%.2lf+(%.2lf)lnx)",a0,a1);

}

void f9(double *x,double *y,double &a0,double &a1)

{

 double x1[n],y1[n];

 int i;

 for(i=0;i<n;i++)

 {

  x1[i]=1.0/x[i];

  y1[i]=1.0/y[i];

 }

 a0=fa1(x1,y1);

 a1=fa0(x1,y1,a0);

 printf("y=x/(%.2lf+(%.2lf)x)",a0,a1);

}

double fa1(double *x,double *y)

{

 double sx,sy,sxy,sx2;

 int i;

 sx=0;

 for(i=0;i<n;i++)

  sx+=x[i];

 sy=0;

 for(i=0;i<n;i++)

  sy+=y[i];

 sxy=0;

 for(i=0;i<n;i++)

  sxy+=x[i]*y[i];

 sx2=0;

 for(i=0;i<n;i++)

  sx2+=pow(x[i],2);

 return (sxy-1.0/n*sy*sx)/(sx2-1.0/n*sx*sx);

}

double fa0(double *x,double *y,double &a1)

{

 double sx,sy;

 int i;

 sx=0;

 for(i=0;i<n;i++)

  sx+=*(x+i);

 sy=0;

 for(i=0;i<n;i++)

  sy+=*(y+i);

 return 1.0/n*(sy-a1*sx);

}

Отримані результати роботи програми:

3.Отримані результати перевіряємо в математичному пакеті Maple:

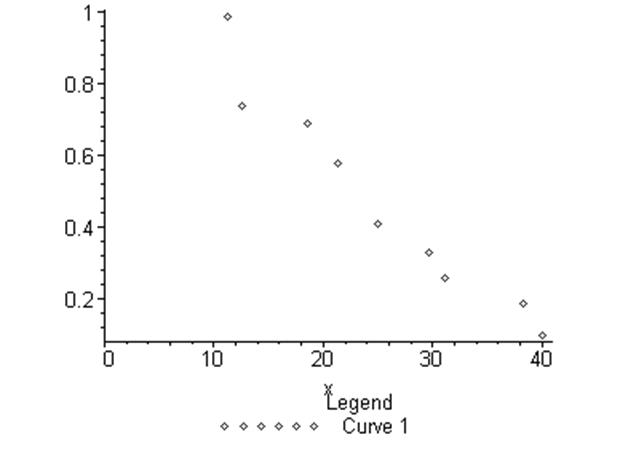
> plot([[11.2,0.99],[12.6,0.74],[18.6,0.69],[21.4,0.58],

    [25,0.41],[29.6,0.33],[31.1,0.26],[38.2,0.19],[40,0.1]],

x=0..41,color=blue,style=POINT, symbol=DIAMOND);

> with(CurveFitting):

>LeastSquares([1/11.2,1/12.6,1/18.6,1/21.4,1/25,1/29.6,1/31.1,1/38.2,1/40], [0.99,0.74,0.69,0.58,0.41,0.33,0.26,0.19,0.1],x, curve=a+b*x);

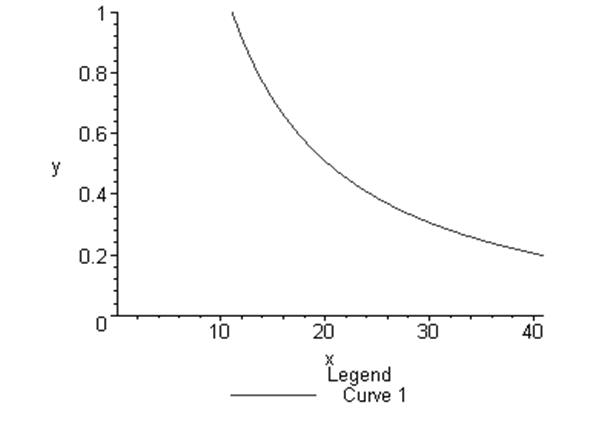
> plot(-0.9859681605e-1+12.1460595456100524*x,x=0..41,y=0..1);