Чисельне розв’язування нелінійних рівнянь (Лабораторна робота № 1)

Лабораторна робота №1

на тему:

«Чисельне розв’язування нелінійних рівнянь»

Варіант 10

Виконала: Татарченко Аліна ІН-91

1. Умова задачі

Завдання. Розв’язати нелінійне рівняння з точністю  :

1 Виділити корені графічно і аналітично.

2 Розв’язати за допомогою методу простої ітерації або методу Ньютона.

0,5^x-3= -(x+1)²

2.Теоретичні відомості

Метод Ньютона (метод дотичних) для наближеного розв’язку рівняння  полягає в побудові ітераційної послідовності ,що збігається до кореня рівняння на відрізку  його локалізації.

                             y

         

                                          

               0           a    x₁           x₀    b                   x

Рисунок 2.3.1

На рисунку 2.3 зображено спосіб отримання першого наближення за методом дотичних: x₁   є точка перетину дотичної, проведеної до кривої в точці з координатами . З прямокутного трикутника, гострий кут якого , маємо

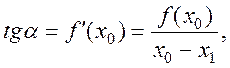 звідки .

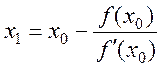Достатні умови збіжності такі. Нехай  - визначена і двічі диференційована на  , причому похідні  зберігають знак на  Тоді , виходячи з початкового наближен-ня  що задовольняє нерівність  ітера-ційна послідовність

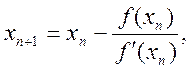
                          (2.7)

збігається до єдиного на  розв’язку рівняння

Для оцінки похибки n-го наближення кореня можна скористатися нерівністю 

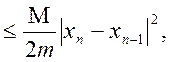                               (2.8)

де  найбільше значення модуля другої похідної  на ; m-найменше значення модуля першої похідної  на .

За необхідності обчислити корінь рівняння з точністю  ітераційну послідовність переривають за умови

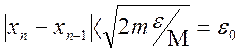                                 (2.9)

 і приймають  за наближене значення кореня

2. Математичне обґрунтування та вибір алгоритму розв’язку

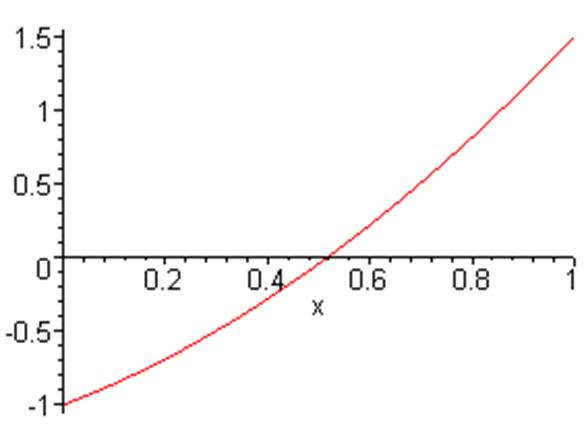
Для того, щоб виділити корені графічно та аналітично можна скористатися засобами програми Maple. Побудувавши графік функції f(x).

Можна визначити відрізок, на якому знаходиться корінь. Також, використовуючи спеціальні функції Maple, можна знайти точний розв’язок рівняння 0,5^x-3= -(x+1)²

, на заданому відрізку (0,1)

Графічно

> plot(0.5^x-3+(x+1)^2,x=0...1);

>

Аналітично

 Для того, щоб аналітично перевірити наявність коренів на відрізку [0;1] необхідно щоб значення функцій на краях відрізка мали різні знаки.

f(0)f(1)<0

 - умова виконується. Отже, на цьому проміжку міститься хоча б 1 корінь.

Перевірка результату в пакетному середовищі Maple.

 > fsolve(0.5^x-3+(x+1)^2,x=0...1);

Для використання методу Ньютона перевіримо його головні умови:

Існує правило: у методі Ньютона за вхідну точку х₀ вибирається той кінець інтервалу , якому відповідає ордината того самого знака, що й знак . Виходячи з нього, х₀= 1.

f’’(1)=ln(0.5)^2*0.5^x+2>0

Так як похідні не дорівнюють 0 і зберігають постійні знаки на проміжку, то, виходячи з початкового наближення х_0, що задовольняє умові , можна обчислити методом Ньютона єдиний корінь рівняння  на проміжку .

3. Програмна реалізація алгоритму

#include<stdio.h>

#include<math.h>

#include<conio.h>

#include<stdlib.h>

double f(double x)

{return pow(0.5,x)-3+pow((x+1),2);}

double fp(double x)

{return log(0.5)*pow(0.5,x)+2*x+2;}

double fpp(double x)

{return log(0.5)*log(0.5)*pow(0.5,x)+2;}

void main()

{double x,xn;

clrscr();

xn=0;

do

{

x=xn;

xn=x-f(x)/fp(x);

}

while(fabs(x-xn)>0.0001);

printf("\nKoren:%6.5f",x);

getch();

}

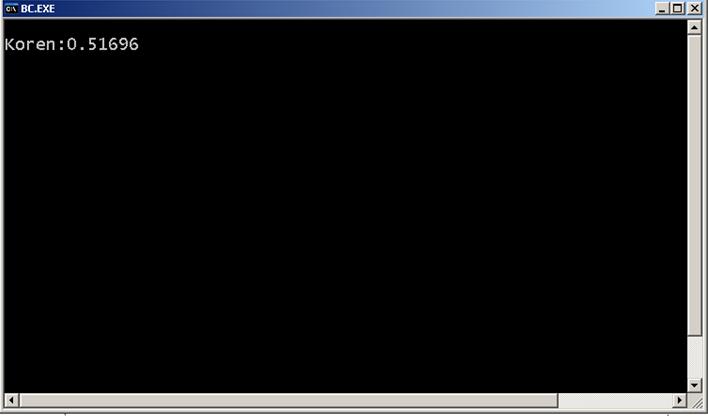
4.Результати роботи програми:

Висновки

У даній лабораторній роботі було виконано розв’язання нелінійного рівняння 0,5^x-3= -(x+1)²

з точністю . Задача була виконана різними методами.

Графічне виділення коренів та аналітичне розв’язання було виконано засобами пакету Maple. Був одержаний результат кореня х = 0.51696на відрізку від 0 до 1.

Також рівняння було розв’язане методом Ньютона, який був програмно реалізований за допомогою мови програмування С. Був одержаний результат кореня х = 0.51696 на відрізку від 0 до 1.

Значення, отримані за допомогою засобів Maple та програмної реалізації методу Ньютона, збігаються, що свідчить про правильне розв’язання рівняння. Обидва методи придатні для розв’язання нелінійних рівнянь і є достатньо універсальними для розв’язування рівнянь схожого типу.