Список теоретичних і практичних питань до комплексної контрольної роботи з дисципліни "Чисельні методи"

Список теоретичних питань до комплексної контрольної роботи.

1.  Похибки чисельного розв’язання задач.
2. Обумовленість та коректність обчислювальної задачі.
3. Стійкість чисельного розв'язку . Способи його визначення.
4. Метод простої ітерації для розв'язання нелінійних алгебраїчних рівнянь . Умови та швидкість збіжності. Геометричне тлумачення. 
5. Метод Ньютона для розв'язання нелінійних алгебраїчних рівнянь . Умови та швидкість збіжності. Геометричне тлумачення.
6. Класифікація методів розв’язання систем лінійних алгебраїчних рівнянь.
7. Метод Гаусса та його модифікації для систем лінійних алгебраїчних рівнянь.
8. Метод простої ітерації для систем лінійних алгебраїчних рівнянь .
9. Метод Зейделя для систем лінійних алгебраїчних рівнянь.
10. Міра обумовленості для систем лінійних алгебраїчних рівнянь.
11. Ітераційні методи для систем нелінійних алгебраїчних рівнянь .
12. Метод градієнтного спуску для систем нелінійних алгебраїчних рівнянь .
13. Задачі інтерполяції та екстраполяції та способи їх розв'язання .Інтерполяційний поліном Ньютона.
14. Інтерполяційні поліноми .. Похибка інтерполяції функції поліномами.
15. Застосування многочленів Чебишева для апроксимації функції.
16. Інтерполяція сплайнами. . Лінійний та кубічний сплайни.
17. Середньоквадратичне наближення функцій. Метод найменших квадратів. 
18. Метод найменших квадратів з поліноміальним базисом. Нормальна система рівнянь.
19. Формули чисельного диференціювання. Апріорні оцінки похибок.
20. Метод Рунге-Ромберга для апостеріорного визначення похибок обчислень.
21. Формули чисельного інтегрування Ньютона-Котеса.
22. Чисельне інтегрування. Формули прямокутників та  трапецій. Порядок похибки.
23. Чисельне інтегрування. Формула Сімпсона. Порядок похибки.
24. Метод Ейлера розв'язання задачі Коші. Похибка методу.
25. Методи Рунге-Кутта 2 та 4 порядку.
26. Багатокрокові методи чисельного розв'язання задачі Коші. Метод прогнозу і корекції..
27. Метод сіток (скінчених різниць) розв’язання крайової задачі для ЗДР другого порядку. Розв’язування сіткових рівнянь методом прогонки
28. Метод сіток розв'язання ДРЧП параболічного типу. Явні та неявні схеми. Проблеми збіжності чисельного розв'язку.
29. Метод сіток розв'язання ДРЧП гіперболічного типу. Проблеми збіжності чисельного розв'язку .
30. Метод Лібмана для розв'язання ДРЧП еліптичного типу. Принцип максимуму для збіжності чисельного розв'язку.

Список практичних завдань до комплексної контрольної роботи.

1. Розв’язати нелінійне рівняння з точністю :

2,2x-2^x=0.

2x-lgx-7=0.                              

3x+cosx+1=0.

2. Методом  Зейделя  розв’язати систему лінійних  алгебраїчних рівнянь  вигляду АХ=В із точністю до 0,0001.

А				В
-0,68	-0,16	-0,08	0,15	-2,42
0,16	-1,23	0,11	-0,21	-1,43
0,05	-0,08	-1,00	0,34	0,16
0,12	0,14	-0,18	-0,94	-1,62

А				В
-1,00	0,08	-0,23	0,32	-1,34
0,16	-1,23	0,18	0,16	2,33
0,15	0,12	-0,68	-0,18	-0,34
0,25	0,21	-0,16	-0,97	-0,63

А				В
-0,94	0,18	0,33	0,16	-2,43
0,32	-1,00	0,23	-0,35	1,12
0,16	-0,08	-1,00	-0,12	-0,43
0,09	0,22	-0,13	-1,00	-0,83

3. Розв’язати  систему нелінійних рівнянь з точністю

 

      

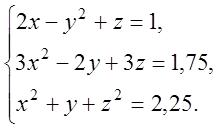
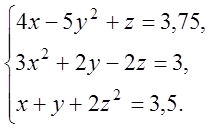
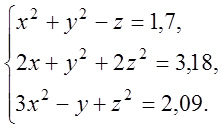
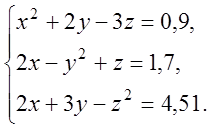
4. Аналітично описати результати 9експериментів, у кожному з яких на вхід системи подається значення параметра Х, а на виході реєструється реакція У.

1 Вибрати вигляд функції.

2 Методом найменших квадратів знайти коефіцієнти.

Таблиця 5.1

X		0,1     0,2      0,3     0,4     0,5     0,6    0,7    0,8   0,9
Y		34,5   18,7   15,1   11,3  12,44  11,9   6,7    4,3    2,
X		0,75  0,78   0,83  0,88  0,93  0,98  1,03  1,21  1,45
Y		10     32,5    47,7  46,1    90   91    95,6   98,2  102
X		1       10       20      30     40     50     60     70     80
Y		33,5    37     41,2  46,1     50   52,9  56,8  64,3 69,9

5. Для функції  y=f(x), що задана таблично, побудувати інтерполяційний многочлен і  сплайн. Обчислити в заданій точці  x^* значення функції і встановити, якою з інтерполюючих функцій доцільніше скористатися.

Значення	x*
x        0            1           2             3             4	1,5
y        1           4          15            40          85
x        1           2           3             4              5	2,4
y       0,8        3           8             17        31,2
x        0          1           2              3              4	3,2
y       0,5        2          7,5           20        42,5

6. Обчислити інтеграл за формулою Сімпсона з точністю =0,001.

 .

  .

 .

.

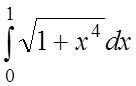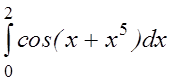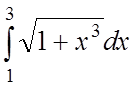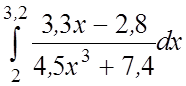7. Чисельно розв’язати задачу Коші для диференціаль-ного рівняння  першого порядку з точністю =0,00001 ,викорис-товуючи метод Рунге- Кутта  4-го порядку:

.

.

.

.

8. Чисельно розв’язати крайову задачу для звичайного диференціального рівняння з точністю

         

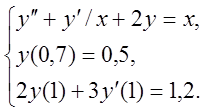
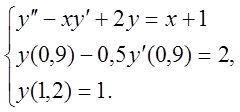
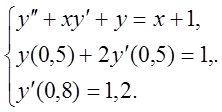
9. Визначити міру обумовленості та стійкість розв’язків системи лінійних алгебраїчних рівнянь АХ=В .

А				В
-0,68	-0,16	-0,08	0,15	-2,42
0,16	-1,23	0,11	-0,21	-1,43
0,05	-0,08	-1,00	0,34	0,16
0,12	0,14	-0,18	-0,94	-1,62

А				В
-1,00	0,08	-0,23	0,32	-1,34
0,16	-1,23	0,18	0,16	2,33
0,15	0,12	-0,68	-0,18	-0,34
0,25	0,21	-0,16	-0,97	-0,63

А				В
-0,94	0,18	0,33	0,16	-2,43
0,32	-1,00	0,23	-0,35	1,12
0,16	-0,08	-1,00	-0,12	-0,43
0,09	0,22	-0,13	-1,00	-0,83