Задания на «4» по численным методам.
№1
Розв’язати нелінійне рівняння 2x+5x-3=0 з точністю e=0,0001.
> fsolve(2^x+5*x-3,x);
х=0,3458;
№2
Розв’язати СЛАР 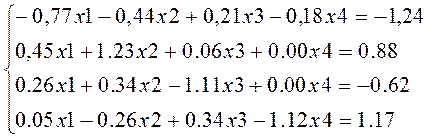 з
точністю
з
точністю ![]()
> solve({-0.77*x1-0.44*x2+0.21*x3-0.18*x4=-1.24, 0.45*x1+1.23*x2+0.06*x3+0.00*x4=0.88, 0.26*x1+0.34*x2-1.11*x3+0.00*x4=-0.62, 0.05*x1-0.26*x2+0.34*x3-1.12*x4=1.17});
![]()
Ответ: x1=2.0891 x2=-0.0985 x3=1.0177 x4=-0.6196
№3
Розв’язати систему нелінійних рівнянь з точністю e=0,0001.
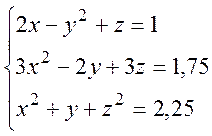
> fsolve({2*x-y^2+z=1, 3*x^2-2*y+3*z=1.75, x^2+y+z^2=2.25});
Ответ: ![]()
№4
За результатами N експериментів необхідно одержати наближення y=j(x), яке апроксимує залежність у від x.
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Xi |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
Yi |
34,5 |
18,7 |
15,1 |
11,3 |
12,44 |
11,9 |
6,7 |
4,3 |
2 |
Y=14.85 -3.71X
№5
Для функції y=f(x), яка задана в таблиці, побудувати інтерполяційний многочлен. Обчислити в заданій точці x*=1,5 значення функції.
|
X |
0 |
1 |
2 |
3 |
4 |
|
Y |
1 |
4 |
15 |
40 |
85 |
Решение:
> interp([0, 1, 2, 3, 4], [1, 4, 15, 40, 85],x);
Р4=![]()
P4(1.5)=8.125,
№6
Для функції y=f(x), яка задана в таблиці, побудувати сплайн. Обчислити в заданій точці x*=1,5 значення заданої функції.
|
X |
0 |
1 |
2 |
3 |
4 |
|
Y |
1 |
4 |
15 |
40 |
85 |
> spline([0, 1, 2, 3, 4], [1, 4, 15, 40, 85],x,cubic);
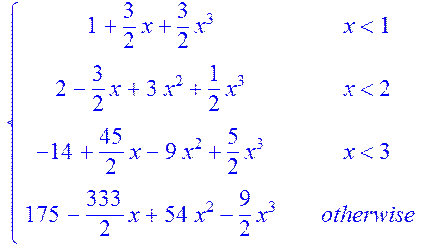
[1;2] S3(1.5)=8.1875
№7
Обчислити інтеграл 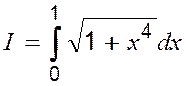 з
точністю
з
точністю ![]() .
.
> evalf(int(sqrt(1+x^4),x=0..1));
I = 1.089
№ 8
Чисельно розв’язав задачу Коші для диференціального рівняння першого порядку з точністю e=0,00001, одержати у(1)
![]()
![]()
> ordev=4:
> a:=diff(y(x),x)=x+y(x)^2:
> cond:=y(0)=0.5:
> rez:=dsolve({a,cond},y(x),numeric);
![]()
> rez(1);
![]()
у(1)= 2.12785
№9
Чисельно розв’язавши крайову задачу, одержати у(1).
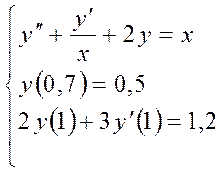
> sys:=diff(y(x),x$2)+(diff(y(x),x)/x)+2*y(x);
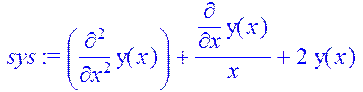
> init:=2*y(1)+3*D(y)(1)=1.2, y(0.7)=0.5;
![]()
> rez:=dsolve({sys,init},y(x),numeric,output=listprocedure);
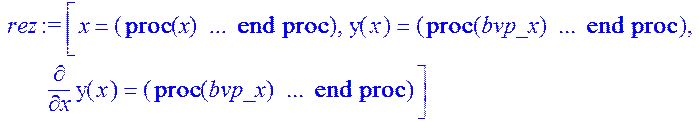
> rez(1);
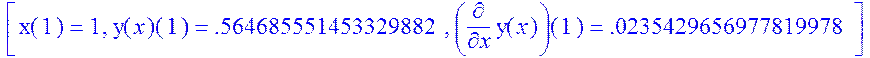
Ответ
![]()
№10
По заданим результатам 6-ти експериментів одержати функцію, яка передбачає реакцію системи за числовими значеннями вхідних параметрів
|
№ експер |
Вхід
|
Вхід
|
Вхід
|
Вхід
|
Вихід |
|
1 |
1 |
-0.2 |
0 |
1 |
0.5 |
|
2 |
0.1 |
1 |
-0.1 |
2 |
-0.5 |
|
3 |
0.3 |
-0.5 |
1 |
3 |
2 |
|
4 |
-0.1 |
0.6 |
0.2 |
2 |
1 |
|
5 |
-0.15 |
1 |
0.4 |
2 |
0.4 |
|
6 |
0 |
0.1 |
-0.05 |
1.5 |
-1 |
![]() - вхід.
- вхід.
F(u)=-0.63![]() -0.02
-0.02![]() -0.84
-0.84![]() +0.47
+0.47![]() ;
;
№11
Розв’язати нелінійне рівняння за допомогою методу Ньютона з точністю e=0,0001 на інтервалі (0;1)
e-2x-2x+1=0
Перевірити, що даний інтервал містить тільки один корінь (вставити знак > або <)
1. F(0) __ 0
2. F(1) __ 0
3. F’(x) __ 0, xÎ(0;1)
4. F”(x) __ 0, xÎ(0;1)
5. Обчисліть початкове наближення Х0 з точністю до десятих
6. Обчисліть перше наближення х1 з точністю до десятих
7. Обчислите корінь рівняння з точністю e=0,0001
Х*» _________
Ответ:
Перевірити, що даний інтервал містить тільки один корінь (вставити знак > або <)
1.F(0) __ 0 ( > )
2.F(1) __ 0 ( < )
3.F’(x) __ 0, xÎ(0;1) ( < )
4.F”(x) __ 0, xÎ(0;1) ( > )
5 Початкове наближення Х0=___ (0)
Вибираємо початкове наближення
кореня ![]() так, щоб
так, щоб ![]() Вибираємо
Вибираємо
![]() , тому що
, тому що ![]() .
.
6.Обчислите перше наближення х1
х1=____ ( 0.5)
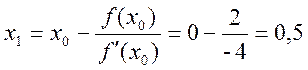
7. Обчислите корінь рівняння з точністю e=0,0001
Х*» _________ ( 0.6392 )
Решение:
> rez:=fsolve((exp(-2*x))-2*x+1,x);
![]()
> diff((exp(-2*x))-2*x+1,x);
![]()
> diff(diff((exp(-2*x))-2*x+1,x),x);
![]()
№12
Розв’язати
нелінійне рівняння за допомогою методу простих ітерацій з точністю ![]() на інтервалі (0;1)
на інтервалі (0;1)
e-2x-2x+1=0
Перевірити, що даний інтервал містить тільки один корінь (вставити знак > або <)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.