Математика \ Численные методы

Тестові завдання на 4 бали з дисципліни "Числові методи", страница 2

1. F(0) ___ 0

2. F(1) ___ 0

3. F’(x) ___ 0, xÎ(0;1)

4. F”(x) ___ 0, xÎ(0;1)

5. Обчислите перше наближення х1, якщо початкове наближення Х0=1

х1=____

6. Обчислите корінь рівняння з точністю (е=0,0001)

Х^*» ____

Перевірити, що даний інтервал містить тільки один корінь (вставити знак > або <)

1.F(0) __ 0 ( > )

2.F(1) __ 0 ( < )

3.F’(x) __ 0, xÎ(0;1) ( < )

4.F”(x) __ 0, xÎ(0;1) ( > )

5. Обчислите перше наближення х1, якщо початкове наближення Х0=1

Замінимо наше рівняння e^-2x-2x+1=0 на еквівалентне йому: ---- x=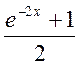

х1===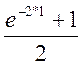0,567668

х1=____ ( 0.5677

6. Обчислите корінь рівняння з точністю (е=0,0001)

Х^*» 0.6392

Решение:

> rez:=fsolve((exp(-2*x))-2*x+1,x);

> diff((exp(-2*x))-2*x+1,x);

> diff(diff((exp(-2*x))-2*x+1,x),x);

№13

Розв’язати систему лінійних рівнянь методом простих ітерацій з точністю е=0,001

5x1- x2+2x3 = 14,7

x1-4x2- x3 = 8,1

2x1-2x2+10x3= 38,4

а) Знайти перше наближення коренів системи { }, якщо (з точністю е=0,001)

X⁽¹⁾₁= __________ ( 2.940)

X⁽¹⁾₂= __________ ( -2.025)

X⁽¹⁾₃= __________ ( 3.840)

Решение:

X1=(14,7+x2-2x3)/5=2.940, подставляем

X2=(8,1-x1+x3)/(-4)= -2.025 подставляем

X3=(38,4-2x1+2x2)/10 подставляем

б) Знайти корені СЛАУ з точністю е=0,001

X^*₁= __________ ( 1.200)

X^*₂= __________ ( -2.500)

X^*₃= __________ ( 3.100)

Решение

> solve({5*x1-x2+2*x3=14.7, x1-4*x2-x3=8.1, 2*x1-2*x2+10*x3=38.4});

№14

Розв’язати систему лінійних рівнянь методом Зейделя з точністю е=0,001

5x1- x2+2x3 = 14,7

x1-4x2- x3 = 8,1

2x1-2x2+10x3= 38,4

а) Знайти перше наближення коренів системи { }, якщо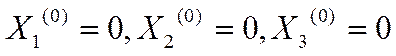

X⁽¹⁾₁= __________ ( 2.940)

X⁽¹⁾₂= __________ ( -1.290)

X⁽¹⁾₃= __________ ( 2.994)

Решение:

X1=(14,7+x2-2x3)/5=2.940, подставляем

X2=(8,1-x1+x3)/(-4)= -1.290 подставляем

X3=(38,4-2x1+2x2)/10=2.994 подставляем

б) Знайти корені СЛАУ з точністю е=0,001

X^*₁= __________ ( 1.200)

X^*₂= __________ ( -2.500)

X^*₃= __________ ( 3.100)

№15

Використовуючи метод скінчених різниць, розв’язати крайову задачу для звичайного диференціального рівняння з точністю . Крок інтегрування 0,1.

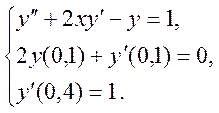
Записати коефіцієнти для різницевої схеми через кому, без пропусків з точністю до тисячних

(крайова умова для х=0.1) a₁₁ y₀ + a₁₂ y₁ + a₁₃ y₂ + a₁₄ y₃ = b₁

a_{11= -1}a_12=0.2 a₁₃₌₀a₁₄₌₀

(крайова умова для х=0.4) a₂₁ y₀ + a₂₂ y₁ + a₂₃ y₂ + a₂₄ y₃ = b₂

a₂₁₌₀a₂₂₌₀a_{23= -1}a₂₄₌₁

(рівняння для х=0.2) a₃₁ y₀ + a₃₂ y₁ + a₃₃ y₂ + a₃₄ y₃ = b₃

a₃₁₌₁₀₀ a_32=-205 a₃₃₌₁₀₄a₃₄₌₀

(рівняння для х=0.3) a₄₁ y₀ + a₄₂ y₁ + a₄₃ y₂ + a₄₄ y₃ = b₄

a₄₁₌₀a₄₂₌₁₀₀a_43=-207 a₄₄₌₁₀₆

№16

Задана система нелінійних рівнянь

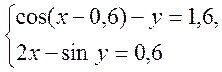
та початкове наближення х0=0,2, у0=-1 Розв’язати цю систему з точністю e=0,0001 методом простих ітерацій.

> fsolve({cos(x-0.6)-y=1.6, 2*x-sin(y)=0.6});

X=______ (-0,0627)

Y=______ (-0,8117)

№17

Задана система нелінійних рівнянь

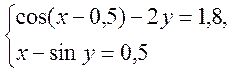
та початкове наближення х0=0, у0=-1 Розв’язати цю систему методом простих ітерацій.

Знайти перше наближення коренів системи X⁽¹⁾, Y⁽¹⁾з точністю e=0,0001.

> fsolve({cos(x-0.5)-2*y=1.8, x-sin(y)=0.5});

Записати розв’язок системи

1) X=______ (0,0689)

Y=______ (-0,4458)

2)X⁽¹⁾=(0,6+sin(0))/2=0,3000 Y1=COS(-0,6)-1,6= -0,77466

№18

Для функції y=f(x), що задана таблично, обчислити в заданій точці x^*= 1.5 значення функції .

Значення

x 0 1 2 3 4

y 1 4 15 40 85

> interp([0, 1, 2, 3, 4], [1, 4, 15, 40, 85],x);

Р4=

P₄(1.5)=8.125,

№19

Для функції y=f(x), яка задана таблично, обчислити у точці x^* =2,8 значеня функції за допомогою полінома Лагранжа з точністю e=0,001.

x 0 1 2 3

y -5 -7 -3 13

> interp([0, 1, 2, 3], [-5, -7, -3, 13],x);

8,552

№20

Задана система нелінійних рівнянь

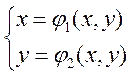
Оберіть вірні умови збіжності: Норма <1

1 2

Скачать файл