Розв’язування систем лінійних алгебраїчних рівнянь. Абсолютна величина і норма матриці, страница 5

При обчисленнях за формулами (13) треба буде виконати приблизно 1/2n² арифметичних дій. Зведення системи (11) до вигляду (12) можна виконати, послідовно заміняючи рядки матриці системи їх лінійними комбінаціями. Перше рівняння не змінюється. Віднімемо з другого рівняння системи (11) перше, помножене на таке число, щоб звернувся в нуль коефіцієнт при x₁. Потім у такий же спосіб віднімемо перше рівняння з третього, четвертого і т.д. Тоді виключаться всі коефіцієнти першого стовпця, що лежать нижче головної діагоналі. Потім за допомогою другого рівняння виключимо з третього, четвертого і т.д. рівнянь коефіцієнти другого стовпця. Послідовно продовжуючи цей процес, виключимо з матриці всі коефіцієнти, що лежать нижче головної діагоналі.

Запишемо загальні формули процесу. Нехай проведене виключення коефіцієнтів з k-1 стовпця. Тоді залишилися такі рівняння з ненульовими елементами нижче головної діагоналі:

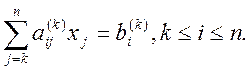                      (14)

Помножимо k-й рядок на число

                               (15)

і віднімемо від m-го рядка. Перший ненульовий елемент цього рядка звернеться в нуль, а інші зміняться за формулами

                (16)

     

Виконуючи обчислення за цими формулами при всіх зазначених індексах, виключимо елементи k-го стовпця. Будемо називати таке виключення циклом процесу. Виконаннявсіх циклів називається прямим ходом виключення.

Запишемо трикутну систему, що виходить після виконання всіх циклів. При приведенні системи до трикутного вигляду звільняться клітки в нижній половині матриці системи (11). Трикутна система легко розв’язується зворотним ходом за формулами (13).

Виключення за формулами (15) не можна проводити, якщо в ході розрахунків на головній діагоналі виявився нульовий елемент  Але в першому стовпці проміжної системи (14) всі елементи не можуть бути нулями: це означало б, що detA=0. Перестановкою рядків можна перемістити ненульовий елемент на головну діагональ і продовжити розрахунки.

Для зменшення обчислювальної похибки можна кожне повторення зовнішнього циклу починати з вибору максимального за модулем елемента в k-тому стовпці (головного елемента) і перестановки рівняння з головним елементом так, щоб він виявився на головній діагоналі. Цей варіант називається методом Гаусса з вибором головного елемента.

У якості однієї з характеристик ефективності того чи іншого алгоритму використовують обчислювальні витрати, вимірювані кількістю елементарних операцій, які необхідно виконати для одержання розв’язку.

Для прямого ходу методу Гаусса число арифметичних операцій, відповідно до формул (15), (16), дорівнює

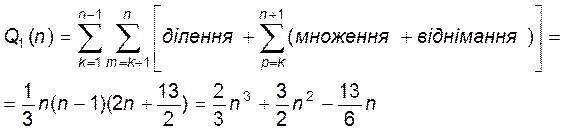
Для зворотного ходу за формулами (13) число арифметичних операцій дорівнює

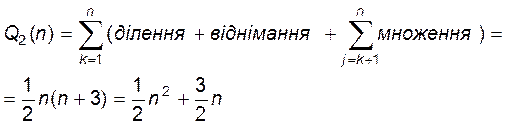
Загальні обчислювальні витрати методу Гаусса:

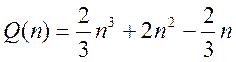
Таким чином, .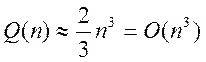

Виконання прямого ходу методу Гаусса дозволяє також обчислити значення визначника матриці системи.

При заміні рядків матриці їхніми лінійними комбінаціями значення визначника не змінюється. Знак змінюється при кожній перестановці рядків. Для трикутної матриці величина визначника дорівнює добутку елементів, що стоять на головній діагоналі. Тому визначник обчислюється за формулою:

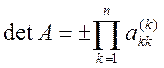
Метод Гаусса може бути використаний для отримання оберненої матриці. Позначимо її елементи через a_jm. Тоді співвідношення A ^. A^-1 = E можна записати так:

.

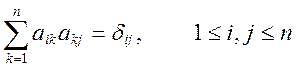Видно, що якщо розглядати j-й стовпець оберненої матриці як вектор, то він є розв’язком лінійної системи вигляду (11) з матрицею A і спеціальною правою частиною (у якій на j – м місці стоїть одиниця, а на інших нулі). Таким чином, для обертання матриці треба розв’язатити n систем лінійних рівнянь з однаковою матрицею A і різними правими частинами. Зведення матриці A до трикутної виконується при цьому тільки один раз, а праві частини перетворюються за формулами (15)-(16).

Перетворення матриці вимагає порядку операцій. Дії по перетворенню правих частин систем і зворотний хід методу Гаусса повторюються 7n разів, а однократне перетворення правих частин і зворотний хід вимагають порядку  операцій. Отже, сумарні обчислювальні витрати на пошук оберненої матриці складають: .