Розв’язування систем лінійних алгебраїчних рівнянь. Абсолютна величина і норма матриці, страница 6

Обертання матриці зводиться до розв’язку n систем лінійних рівнянь, але вимагає лише приблизно втроє більше дій, ніж розв’язок однієї системи рівнянь. Це обумовлюється тим, що при розв’язку лінійної системи велика частина обчислень пов'язана з приведенням матриці до трикутного вигляду, а це при обертанні матриці робиться тільки один раз. Зворотний хід і перетворення правих частин виконуються набагато швидше.

Узагалі, метод Гаусса застосовується для розв’язку будь-яких систем лінійних рівнянь, тому що він дозволяє одержати розв’язок системи, якщо він існує (включаючи випадок, коли частина невідомих є вільними і розв’язків у системи є безліч) і знайти відсутність розв’язку (коли система несумісна). В останньому випадку після чергового k-го кроку прямого ходу всі елементи матриці системи нижче k-ого рядка дорівнюють нулю, а серед відповідних компонентів вектора b є ненульові значення.

Метод Краута

Якщо дуже коротко, то суть методу Краута, або LU-розкладання полягає в тому, що це своєрідний перезапис методу Гауса. Суть в тому, що можна явно виділити два етапи, у яких один робить перетворення з матрицею А системи, інший – з вектором правих частин b. Отже, нехай дана СЛАР  A∙x=b, наприклад, система розміром 4´4. Запишемо розширену матрицю системи

Тоді, за Гауссом  можна явно виділити два етапи (тобто два кроки) – прямий хід (ПХ) і зворотний (ЗХ)

1)  ПХ: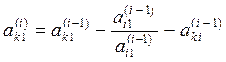

  2)   ЗХ:

На прямому ході, ми робимо, так звані “виключення”, тобто приводимо матрицю до трикутного вигляду. Тепер легко знайти x₄, а потім і x₃ і т.д. Це був зворотний хід метода Гаусса. Всі ці перетворення виконувались не із самою матрицею, а з розширеною матрицею.

Головна ідея і потреба методу LU – декомпозиції полягає в тому, щоб розділити окремо етап перетворення коефіцієнтів матриці, і окремо етап перетворення вектора правих частин.

Отут виникає відразу два питання: а) навіщо це потрібно?; б) як це зробити?

Навіщо це потрібно? Це дозволяє один раз перетворити матрицю системи, а потім кілька разів розв’язувати декілька систем з різними правими частинами. Обчислювальні витрати при цьому будуть зводитися тільки до зворотного ходу.

Як це зробити? Запишемо A×x= b, як

L×U×x= b,

Тобто ми припускаємо, що якимсь чином матрицю А можна представити як добуток двох матриць: А = L×U. Позначимо

U×x= y,

І отже                                      L×y= b.

Отже, прямий хід методу LU-декомпозицiї складається з розкладу матриці A на нижню L та верхню U трикутні матриці – це прямий хiд.

Потiм визначається вектор y на основі співвідношень:

На зворотному ході метода LU-декомпозицiї розв’язується рівняння U×x= y. З урахуванням того, що U – трикутна матриця

Отже, LU-розкладання є просто свого роду іншою формою запису еквівалентних перетворень матриці за методом Гаусса, але проведених з урахуванням умови А = L×U.

Розглянемо схему LU-розкладання.

u_ij = a_ij – 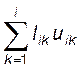, j = 1..n, i = 1..j

l_ii = 1, i = 1..n;l_ij = a_ij – 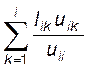, j = 1..n, i = j+1..n. (1.5)

Визначимо нижню трикутну матрицю L з одиничною головною діагоналлю:

L =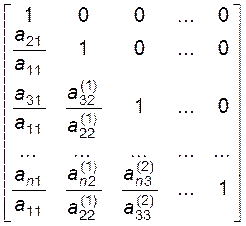

Матриця U має вигляд

U =

Прямою підстановкою можна перевірити правильність розкладання початкової матриці А в добуток.

A = LU(1.6)

Остання формула і є LU-декомпозицією або розкладанням матриці A. Взагалі очевидно, що розв'язок початкової системи рівнянь еквівалентний розв'язку двох систем з трикутними матрицями

Lg = b(1.7)

Ux = g(1.8)

Систему (1.7) розв’язуємо прямою підстановкою:

g_i = b_i  – ;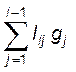

а (1.8) - зворотною підстановкою:

x_i = (g_i – 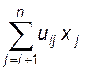) / u_ii.

Теорема 1. Для існування LU-розкладання матриці А необхідно й достатньо, щоб у матриці А усі головні мінори були відмінні від нуля.

У довільної невиродженої матриці А головні мінори, тобто

, , …,

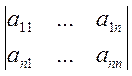
можуть перетворюватися на нуль.

Взагалі, для застосування методу Гаусса до таких матриць або, що те ж саме, одержання LU-розкладання, необхідно переставити рядки так, щоб головні мінори стали відмінними від нуля.