Розв’язування систем лінійних алгебраїчних рівнянь. Абсолютна величина і норма матриці, страница 2

Наведемо без доведення теореми про деякі форми представлення матриць.

Теорема 3. Нехай А –– довільна () – матриця і –– її  різні власні значення з геометричним  та алгебраїчними  кратностями. Тоді для кожного власного значення  існують  натуральних чисел  таких, що

а також невироджена () – матриця Т така, що матриця  яка називається нормальною формою Жордана матриці А, має вигляд

,

де матриці

називаються жордановими клітинками. При цьому числа  з точністю до перестановки однозначно визначені, а матриця Т, взагалі кажучи, визначається неоднозначно.

Розщепимо матрицю Т за стовпчиками відповідно до нормальної форми Жордана:

Тоді із співвідношення  маємо

               .

Позначимо стовпчики - матриці  через  тобто

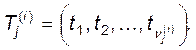
Тоді з означення матриць  дістанемо

,

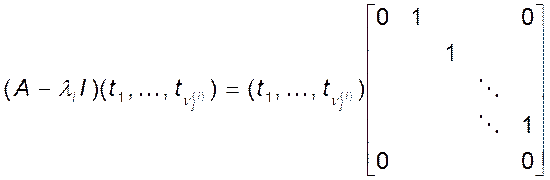або

Зокрема помічаємо, що  є власним вектором матриці А, що відповідає власному значенню . Інші вектори  називаються головними векторами, що відповідають значенню , і ми бачимо, що кожній клітинці Жордана  відповідає один власний вектор і набір головних векторів. В цілому для кожної () – матриці А можна знайти базис простору , який складається з власних та головних векторів матриці А.

Характеристичні поліноми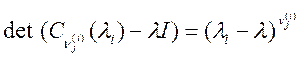

окремих клітинок Жордана  називаються елементарними дільниками матриці А. Таким чином, матриця А має лінійні елементарні дільники тоді і тільки, коли  тобто жорданова нормальна форма матриці А є діагональною матрицею. У цьому разі А називається матрицею, що зводиться до діагонального вигляду, або матрицею, що припускає нормалізацію, тобто в  є базис, який складається лише з власних векторів матриці А, а головні вектори не з’являються. Отже, кожну матрицю яка має різні власні значення, можна звести до діагонального вигляду за допомогою перетворення подібності.

Якщо в перетворенні подібності  припускати, що Т не довільні несингулярні матриці, то А у загальному випадку не може бути зведена до форми Жордана. Для унітарних матриць Т, тобто має місце така теорема.

Теорема 4 (теорема Шура). Для довільної матриці  існує унітарна матриця така, що

де –– власні значення матриці А.

Якщо А=А*, тобто А є ермітовою матрицею, то  є також ермітовою і з теореми 4 випливає така теорема.

Теорема 5. Для довільної ермітовоїматриці А існує унітарна матриця  така, що

.

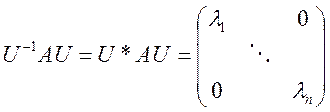При цьому власні значення матриці А є дійсними,  а і-й стовпчик  матриці є власним вектором, відповідним , тобто А має  лінійно незалежних власних векторів.

Узагальненням ермітових є нормальні матриці, для яких

Теорема 6. Матриця  є нормальною (А*А=АА*) тоді і лише тоді, коли існує унітарна матриця  така, що

,

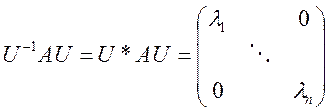тобто нормальні матриці можна звести до діагонального вигляду, вони мають  лінійно незалежних ортогональних векторів ,які є стовпчиками матриці

Теорема 7. Нехай . Тоді:

1) існує унітарна () – матриця  та унітарна () – матриця  такі, що матриця  є діагональною () – матрицею вигляду де –– відмінні від нуля сингулярні числа матриці ––ранг матриці А;

2) відмінними від нуля сингулярними числами матриці А* є також . Розвинення  називається сингулярнозначним зображенням матриці А.

Унітарні матриці  та  можна інтерпретувати таким чином: стовпчики матриці  являють собою  ортогональних власних векторів ермітової () – матриці АА*, а стовпчики  є ортогональними власними векторами ермітової () – матриці А*А, бо  Діагональна () – матриця

є псевдооберненою до , або оберненою матрицею Мура –– Пенроуза, тобто матрицею, що задовольняє співвідношення:

а)

б)

в)

Тому, як легко помітити, () – матриця є в силу того, що вона одна, оберненою до А.

Нехай власний вектор  є спряженим до :

Лема 1. Нехай є простим власним значенням матриць що відповідають власним векторам  та . Тоді існує неперервне диференційоване відображення

деякого околу  з простору матриць  з центром в А таке, що  і  є простим власним значенням матриці В для всіх  причому

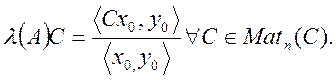
Теорема 8. Абсолютне та відносне числа обумовленості задачі обчислення простого власного значення  матриці  стосовно матричної норми  виражаються формулами

де  –– власний вектор матриці А, що відповідає власному значенню  –– спряжений до нього власний вектор матриці А*, тобто Зокрема проблема власних значень для нормальних матриць є добре обумовленою з числом обумовленості .