Розв’язування систем лінійних алгебраїчних рівнянь. Абсолютна величина і норма матриці, страница 3

Приклад матриці

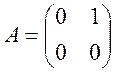
з власними значеннями  та збуреної матриці

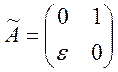
з власними значеннями  показує, що для несиметричних матриць проблема власних значень може бути, взагалі кажучи, погано обумовленою. Дійсно,

тобто задача обчислення власного значення  матриці А стосовно абсолютної похибки взагалі не є коректно поставленою задачею.

Інший приклад , розглянутий у вступі, показує, що обчислення власних значень як коренів характеристичного многочлена хоча теоретично і можливе, але потребує великої обережності. Тому на практиці, як правило, застосовують інші методи.

Стійкі матриці.

Матриця А називається стійкою, якщо її власні значення мають від’ємні дійсні частини.

Задача перевірки матриці на стійкість є досить важкою, і дотепер не отримано скільки-небудь простого її розв’язку. Цю задачу ускладнює та обставина, що ми не стільки зацікавлені в її розв’язку для даної конкрентной матриці А, скільки в одержанні умов, що дозволяли б нам стверджувати, що різні представники класу матриць А( ) є стійкими. Питання такого типу постійно виникають при конструюванні систем керування, у математичній економіці, а також при вивченні обчислювальних алгоритмів.

          Якщо характеристичний многочлен матриці А отриманий, то існує безліч критеріїв, за допомогою яких ми можемо судити, чи мають власні значення матриці А від’ємні дійсні частини чи ні. Очевидно, найбільш корисним з них є критерій Гурвіца.

          Розглянемо рівняння:

            ( 1)

Для многочлена, що стоїть в правій частині ( 1 ), складемо нескінченну таблицю

а₁          1      0      0      0      0 …

а₃          а₂        а₁       1     0      0 …

 а₅       а₄           а₃     а₂       а₁   1 …

   а₇          а₆          а₅    а₄        а₃        а₂ …,

…………………

де коефіцієнти  покладаються рівними нулю, якщо k > N. Для того щоб усі корені рівняння ( 1) мали від’ємні дійсні частини, необхідно і достатньо, щоб усі визначники з послідовності

h₁=|a₁|, h₂=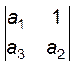              ,…… були додатніми.

          Не існує скільки-небудь простого доведення цього критерію. Причина, чому він не завжди є ефективним, полягає в необхідності обчислення визначника , що є вкрай небажаним, якщо порядок матриці А досить великий.

Системи лінійних алгебраїчних рівнянь

Розглянемо систему вигляду

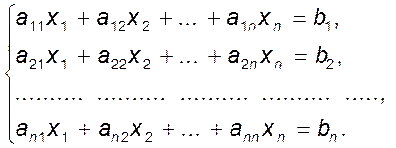                        (3.1)

Її матричний вигляд

АХ=В.                                            (3.2)

Тут  А – {[],(i,j=)}-матриця коефіцієнтів системи,

B= ,               X= - вектори-стовпці.

Відомо, що система (11) має єдиний розв’язок, якщо її матриця невироджена (тобто визначник матриці A відмінний від нуля).

У випадку виродженості матриці система може мати нескінченне число розв’язків (якщо ранг матриці A і ранг розширеної матриці, отриманої додаванням до A стовпця вільних членів рівні) чи не мати розв’язків зовсім (якщо ранг матриці A і розширеної матриці не збігаються)

Методи чисельного розв’язку СЛАР поділяються на точні і наближені. Метод вважають точним, якщо, нехтуючи похибками округлення, він дає точний результат після виконання певної кількості обчислювальних операцій. Математичні пакети прикладних програм для ПЕОМ містять стандартні процедури розв’язку СЛАР такими поширеними точними методами, як метод Гаусса, метод Жордана-Гаусса, квадратного кореня та інші.

До наближених методів розв’язку СЛАР відносяться метод простої ітерації, метод Зейделя, метод релаксації та інші. Вони дозволяють отримати послідов-ність  наближень до розв’язку  таку, що .

Ітераційні методи прості, легко програмуються і мають малу похибку округлення, але вони дають збіжну послідовність наближень тільки за виконання певної умови, що гарантує виконання принципу стискаючих відображень. Це достатня умова збіжності ітераційного процесу: модулі діагональних коефіцієнтів для кожного рівняння системи не повинні бути менше, ніж сума модулів усіх інших коефіцієнтів при невідомих

.                                      (3.3)

Оцінка похибки і міра обумовленості

Припустимо, що матриця системи лінійних рівнянь і вектор правих частин задані неточно і замість пред'явленої до розв’язку системи

A^. x=b                                                      (4)

у дійсності розв’язується деяка система