Поєднуючи ці рівності з (5) (l= N-1), одержимо остаточні формули для знаходження невідомих
уi=ai+1 уi+1+ bi+1, i=N-1, N-2, ..., 0,
уN= bN+1, (6)
де коефіцієнти знаходяться за рекурентними формулами:
ai+1=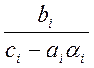 , i=1, 2, …, N-1, a1=
, i=1, 2, …, N-1, a1=![]() (7)
(7)
bi+1=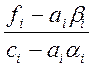 , i=1, 2, ..., N-1; b1=
, i=1, 2, ..., N-1; b1=![]() (8)
(8)
Отже, формули (6)-(8) описують метод Гаусса, що у застосуванні до системи (1) одержав спеціальну назву - метод прогонки. Коефіцієнти ai і bi називаються прогонковими коефіцієнтами, формули (7), (8) описують прямий хід прогонки, а (6) - зворотний хід. Оскільки значення уi знаходяться тут послідовно при переходу від i+1 до i, то формули (6)-(8) називають іноді правою прогонкою.
Метод зустрічних прогонок. Вище були отримані формули правої прогонки для розв’язку системи (1). Аналогічно виводяться формули лівої прогонки:
xi =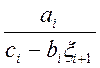 , i=N-1, N-2, ..., 1;
, i=N-1, N-2, ..., 1;
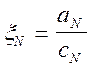 , (9)
, (9)
hi=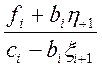 , i=N-1, N-2, ..., 0;
, i=N-1, N-2, ..., 0;  , (10)
, (10)
yi+1=xi+1 уi+hi+1, i=0, 1, ..., N-1; ![]() . (11)
. (11)
Тут значення уi знаходяться послідовно при зростанні індексу i (зліва направо).
Іноді виявляється зручним комбінувати праву і ліву прогонки, одержуючи так званий метод зустрічних прогонок. Цей метод доцільно застосовувати, якщо треба знайти тільки одну невідоме, наприклад ym (0£m£N), або групу невідомих. Одержимо формули методу зустрічних прогонок. Нехай 1£ m£N і за формулами (7)-(10) знайдені a1, a2, ..., am, b1, b2, ..., bm, і xN, xN-1, ..., xm, hN, hN-1, ..., hm. Випишемо формули (6), (11) для зворотного ходу правої і лівої прогонок для i=m-1. Будемо мати систему, з якої знайдемо ym:
ym= .
.
Використовуючи знайдене ym, за формулами (6) для i=m-1, m-2, ..., 0 знайдемо послідовно ym-1, ym-1, ..., y0, а за формулами (11) для i=m, m+1, ..., N обчислимо інші ym+1, ym+2, ...,yN.
Отже, формули методу зустрічних прогонок мають вигляд:
ai+1=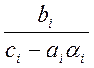 , i=1, 2, ..., m-1, a1=
, i=1, 2, ..., m-1, a1=![]() ,
,
bi+1=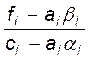 , i=1, 2, ..., m-1, b1=
, i=1, 2, ..., m-1, b1=![]() ,
,
xi =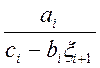 , i=N-1, N-2, ..., m,
, i=N-1, N-2, ..., m, 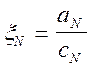 , (12)
, (12)
hi=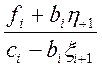 , i=N-1, N-2, ..., m,
, i=N-1, N-2, ..., m,  ,
,
для обчислення прогонкових коефіцієнтів і
уi=ai+1 уi+1+ bi+1, i=m-1, m-2, ..., 0;
уi+1=xi+1 уi+hi+1, i=m ,m+1, ..., N-1; (13)
ym=
для визначення розв’язків.
3.1 Метод простої ітерації
Розглянемо СЛАР у матричному вигляді (3.2) (діагональні коефіцієнти aii відмінні від нуля для всіх i). Зведемо її до вигляду X=CX+D, де C=[cij] - квадратна матриця порядку n:
![]()
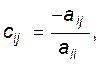
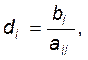
![]() .
.
При цьому СЛАР (3.1) набуде вигляду
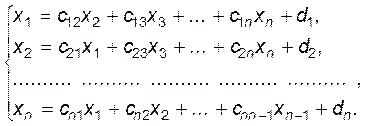 (3.4)
(3.4)
Взявши
довільне початкове наближення ![]() , будуємо ітераційний
процес за формулою
, будуємо ітераційний
процес за формулою ![]() (k=1,2,…).
(k=1,2,…).
3.2 Метод Зейделя
Ітераційний процес Зейделя відрізняється від методу простої ітерації тим, що при розв’язуванні систем вигляду X=CX+D обчислення наступного наближення значення xi при 1<i<n використовує обчислені раніше наближення невідомих x1,x2,…,xi-1… .
У цьому випадку ітераційний процес методу Зейделя має вигляд:
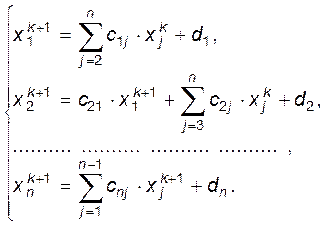 (3.5)
(3.5)
Часто в практичних обчисленнях ітераційний процес припиняють, якщо два послідовних наближення відрізняються менше від наперед заданого числа ∆ у змісті обраної норми:
![]()
тобто коли
наближені розв’язки ![]() і
і ![]()
![]() стануть
стануть
досить близькими і 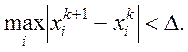 Величина ∆ пов'язана з точністю ε
розв’язання системи співвідношенням
Величина ∆ пов'язана з точністю ε
розв’язання системи співвідношенням  , де
, де![]() - будь-яка канонічна норма матриці з
коефіцієнтів при невідомих у правих частинах рівнянь перетвореної системи:
X=BX+D.
- будь-яка канонічна норма матриці з
коефіцієнтів при невідомих у правих частинах рівнянь перетвореної системи:
X=BX+D.
Приклад. Розв’язати систему 
Розрахунок системи рівнянь двома методами
Метод простої ітерації Метод Зейделя
_________________________________________________________
![]()
![]()
______________________________________________________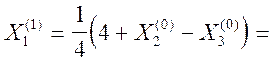
![]()
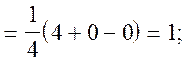
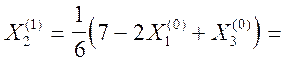

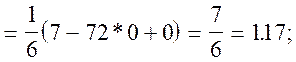
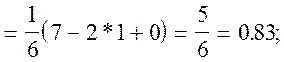
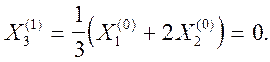

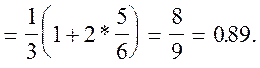
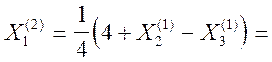
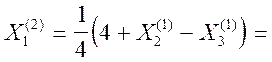
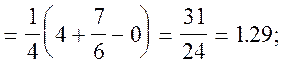
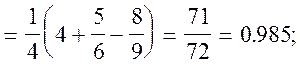
![]()
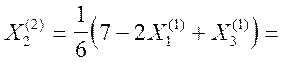
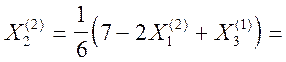
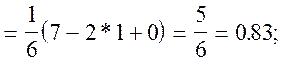

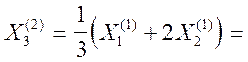
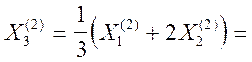

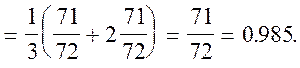 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.