Розв’язування систем лінійних алгебраїчних рівнянь. Абсолютна величина і норма матриці, страница 7

Звичайно, перестановка рядків не проводиться окремо від процедури вилучення, ці два процеси поєднуються в один. Якщо a₁₁=0, переставимо рядки матриці А так, щоб у лівому верхньому куті виявився ненульовий елемент. У першому стовпці такий елемент завжди знайдеться, інакше det А = 0, Якщо після першого кроку дістанемо a₂₂⁽¹⁾ = 0, то виконаємо, як і вище, переставлення: у другому стовпці завжди знайдеться ненульовий елемент, інакше два перших стовпці були б лінійно залежні і det А = 0. Помістимо рядок з ненульовим елементом у другому стовпці на місце другого рядка, тоді a₂₂⁽¹⁾≠0. Продовжуючи цей процес вилучення й переставлення рядків (якщо елемент a_kk^(k-1)=0) до k=n, дістанемо LU-розкладання матриці А з додатковою матрицею Р перестановок рядків:

PA = LU.

Матриця А одержується з одиничної матриці Е перестановкою тих же рядків. Наприклад, перестановці другого та четвертого рядків матриці відповідає

P =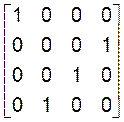

Таким чином ми отримали LUP-розкладання.

Приклад

Розв'яжемо систему рівнянь за схемою LU-розкладання:

Виконаємо дії за алгоритмом і отримаємо матриці L i U у вигляді:

L=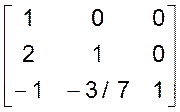, U=.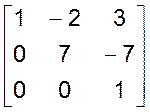

Відповідно до (2.30) маємо

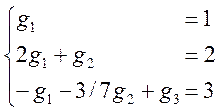
Розв'язуючи цю систему, маємо: g = {1, 0, 4}.

Відповідно до (2.31) маємо

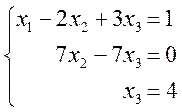
Зворотний хід:

x₁ = 4, x₂ = 4, x₃ = -3.

Метод прогонки.

Це - ще одна модифікація методу Гаусса для систем лінійних алгебраїчних рівнянь спеціального вигляду. Нехай потрібно знайти розв’язок системи трёхточкових рівнянь:

          с₀у₀-b₀y₁=f₀, i=0;   

          -a_iy_i-1+c_iy_i-b_iy_i+1=f_i,          1£ i£ N-1;                                   (1)

          -a_Ny_N-1+c_Ny_N=f_N,   i=N.

          Такі системи виникають при трёхточковій апроксимації крайових задач для звичайних диференціальних рівнянь другого порядку з постійними і змінними коефіцієнтами, а також при реалізації різницевих схем для рівнянь у часткових похідних.

          Переходимо до побудови алгоритму розв’язку системи (1). На першому кроці з усіх рівнянь системи (1) для i=1,2,...,N виключається за допомогою першого рівняння (1) невідоме у₀, потім з перетворених рівнянь для i=2,3, ...,N за допомогою рівняння, що відповідає i=1, виключається невідоме у₁ і т.д. У результаті одержимо одне рівняння відносно у_N. На цьому прямий хід методу закінчується. На зворотному  ході для    i=N-1,N-2, ...,0 знаходиться у_i через уже знайдені у_i+1, y_i+2, ..., y_N і перетворені праві частини.

          Використовуючи підходи методу Гаусса, проведемо  виключення невідомих з (1). Позначивши a₁=b₀/c_0, b₁=f₀/c₀, запишемо (1) :

          y₀-a₁y₁=b₁,                       i=0;

          -a_iy_i-1+c_iy_i-b_iy_i+1=f_i,                    1£ i£ N-1;                       (1’)

          -a_Ny_N-1+c_Ny_N=f_N,              i=N.

Візьмемо перші два рівняння системи (1’)

          y₀-a₁y₁=b₁,            -a_iy_i-1+c_iy_i-b_iy_i+1=f_i.

Помножимо перше рівняння на a₁ і складемо з другим рівнянням. Будемо мати (c₁-a₁a₁₎y₁-b₁y₂=f₁+a₁b_1, або після ділення на c₁-a₁a₁

                у₁-a₂ у₂= b₂,           a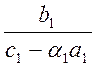₂= ,         b₂=.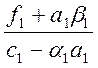

Всі інші рівняння системи (1’) у₀ не містять, тому на цьому перший крок процесу виключення закінчується. У результаті одержимо нову “скорочену” систему

          y₁-a₂y₂=b₂,                       i=1;

          -a_iy_i-1+c_iy_i-b_iy_i+1=f_i,          2£ i£ N-1;                                   (3)

          -a_Ny_N-1+c_Ny_N=f_N,              i=N,

яка не містить невідоме у₀  і має аналогічну (1’) структуру. Якщо ця система буде розв’язана, то невідоме у₀ знайдеться із рівняння y₀-a₁y₁=b₁. До системи (3) можна знову  застосувати описаний спосіб виключення невідомих. На другому кроці буде виключене невідоме у₁ на третьому у₂ і т.д. У результаті l-го кроку одержимо систему для невідомих у_l, y_l+1, ..., y_N 

          y_l-a_l+1y_l+1=b_l+1,                 i=l;

          -a_iy_i-1+c_iy_i-b_iy_i+1=f_i,          l+1£ i£ N-1;                                         (4)

          -a_Ny_N-1+ c_Ny_N = f_N ,                    i=N.

і формули для знаходження у_i c номерами  i£ l-1

          у_i=a_i+1 у_i+1+ b_i+1,    i=l-1, l-2, ..., 0.                                    (5)

Коефіцієнти a_i  і b_i знаходяться за формулами

          a_i+1=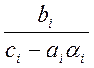, b_i+1= 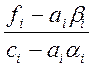,i=1,2, ..., a₁=     b₁= 

Вважаючи в (4) l= N-1, одержимо систему рівнянь для y_N і y_N-1

          y_N-1-a_N у_N= b_N,

         -a_Ny_N-1+ c_Ny_N = f_N ,

з якої знайдемо у_N= b_N+1,                   y_N-1=a_N у+ b_N.