A1. x=b1, (5)
де A1=A+![]() ,b1=b+
,b1=b+![]() . Позначимо розв’язки (4) і (5) через x
і x1
. Позначимо розв’язки (4) і (5) через x
і x1
Оцінимо похибку розв’язку z = x1 - x.
Підставимо вирази для A1, b1 і x1 у (5)
(A+![]() ) (x+z) = b +
) (x+z) = b + ![]()
Віднімаючи (4), одержимо
A z + ![]() .x +
.x + ![]() .z =
.z = ![]()
z = A-1 (![]() -
- ![]() .x -
.x -![]() .
z )
.
z )
||z||<=||A-1||.(||![]() || + ||
|| + ||![]() || .
||x|| + ||
|| .
||x|| + ||![]() || ||z||) (6)
|| ||z||) (6)
Якщо
малі ||![]() || і ||
|| і ||![]() ||, то
варто очікувати і малості ||z||. Тоді доданок
||, то
варто очікувати і малості ||z||. Тоді доданок ![]() .z
має більш високий порядок малості. Звідси випливає оцінка похибки
.z
має більш високий порядок малості. Звідси випливає оцінка похибки
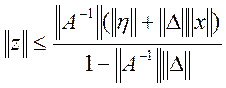 . (7)
. (7)
Досить розповсюджений випадок, коли похибка
матриці системи істотно менше похибки правої частини; як модель цієї ситуації
будемо розглядати випадок точного задання матриці системи. Тоді, вважаючи ![]() = 0 у (7) маємо
= 0 у (7) маємо
||z||<=||A-1||. ||![]() || (8)
|| (8)
Для якісної характеристики зв'язку між похибками правої частини і розв’язку вводиться поняття обумовленості матриці системи. Абсолютні похибки правої частини і розв’язку системи залежать від масштабів, якими вимірюються ці величини і матриця системи. Тому правильніше характеризувати властивості системи через зв'язок між відносними похибками правої частини і розв’язку. Для відносної похибки розв’язку з (8) маємо
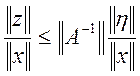 (9)
(9)
Підставляючи оцінку для ||x|| у (9) маємо
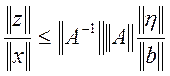 (10)
(10)
Величину ||A-1||||A|| = condА
називають мірою обумовленості матриці. Величина відносної похибки розв’язку при
фіксованій величині відносної похибки правої частини може стати як завгодно
великою при досить великій мірі обумовленості матриці. Число обумовленості
залежить від вибору норми матриці. Будь-яка норма матриці не менше її
найбільшого за модулем власного значення, тобто ||A||>= max |![]() |. Власні значення матриці A і A-1
взаємно обернені; тому
|. Власні значення матриці A і A-1
взаємно обернені; тому 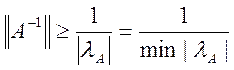 .
.
Таким чином,
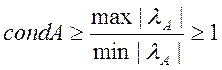 .
.
Системи
рівнянь і матриці з великими значеннями мір обумовленості прийнято називати
погано обумовленими, а з малими - добре обумовленими. Отже, при розв’язуванні СЛАР на ЕОМ обов’язково виникають
похибки заокруглення. Тому фактично маємо розв’язок ![]() деякої
іншої системи
деякої
іншої системи ![]() . На практиці важливо
знати відносну похибку
. На практиці важливо
знати відносну похибку  . Якщо замість
. Якщо замість ![]() брати модель
брати модель ![]() тобто
тобто ![]() в ЕОМ задається точно, то з попередніх
співвідношень випливає
в ЕОМ задається точно, то з попередніх
співвідношень випливає ![]() (
(![]() - є міра невизначеності розв’язку системи
при неточних вхідних даних).
- є міра невизначеності розв’язку системи
при неточних вхідних даних).
Якщо брати модель обчислень
![]() , в якій збурені лише елементи
, в якій збурені лише елементи ![]() , а b –
точне ,то використовуючи співвідношення
, а b –
точне ,то використовуючи співвідношення ![]() -
-![]() =
=![]() (
(![]() )
)![]() , дістаємо
, дістаємо ![]()
![]()
![]()
![]()
![]() (
(![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() cond
cond![]()
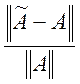 .
.
Якщо С-квадратна матриця така ,що ![]() ,то
існує (І+С)-1, причому ||(І+С)-1||
,то
існує (І+С)-1, причому ||(І+С)-1||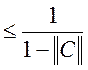
![]()
Так, як ![]()
![]() СЛАР
СЛАР ![]() має лише тривіальний розв’язок, що і
означає невиродженість матриці І+С.
має лише тривіальний розв’язок, що і
означає невиродженість матриці І+С.
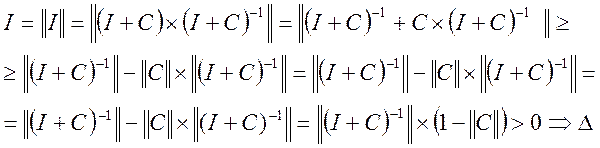 Теорема
Нехай А- невироджена
квадратна матриця, , причому
Теорема
Нехай А- невироджена
квадратна матриця, , причому 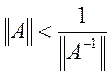 . Тоді , якщо x
та
. Тоді , якщо x
та ![]() є відповідно розв’язками систем Ax=b
та
є відповідно розв’язками систем Ax=b
та ![]()
![]() , де Ã=А+ΔА
, де Ã=А+ΔА ![]() , то має місце оцінка
, то має місце оцінка 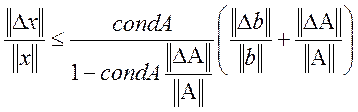
Доведення.Оскільки ![]() , то в
силу леми існує
, то в
силу леми існує ![]() причому
причому 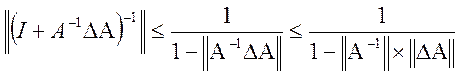
![]()
Знайдемо ![]()
![]()
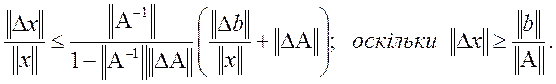 дістаємо шукане.
дістаємо шукане.
.Метод Гауcса
Розглянемо задачу розв’язку системи рівнянь:
 (11)
(11)
чи Ax=b, де A - матриця коефіцієнтів системи, x - вектор невідомих, b - вектор правих частин. Відомо, що розв’язок системи лінійних рівнянь можна виразити за формулами Крамера через відношення визначників. Але обчислення визначника не простіше за розв’язок вихідної системи. Для розв’язку системи порядку n необхідно обчислити (n+1) визначник, тобто обчислення розв’язку за формулами Крамера вимагає в (n+1) раз більше операцій ніж розв’язування системи іншим методом, наприклад методом Гаусса.
Метод Гаусса заснований на приведенні шляхом еквівалентних перетворень вихідної системи (11) до вигляду з верхньою трикутною матрицею.
![]() с11 . x1 + c12x2
+ … + c1n xn =d1
с11 . x1 + c12x2
+ … + c1n xn =d1
0 + c22x2 + … + c2nxn = d2
………………………… (12)
0 + 0 + … + cn-1,n-1xn-1 + cn-1,nxn = dn-1
0 + 0 +……………... +0 +cnnxn = dn
Тоді з останнього рівняння відразу визначаємо
 .
.
Підставляючи його в попереднє рівняння, знаходимо xn-1 і т.д. Загальні формули для отримання розв’язку мають вигляд
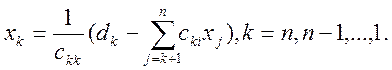 (13)
(13)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.