Поля
Def: Полем называется множество элементов F = {α ,β ,γ ,…} для которых определены 2 алгебраические операции: сложение и умножение, так что сумма и произведение двух любых элементов α, β, принадлежащих F снова принадлежат F. Причем выполнены следующие условия (аксиомы):
A1. α+β=β+α для " α,β Î F (коммутативность)
А2. (α+β)+γ = α+(β+γ) для " α,β,γ Î F(ассоциативность сложения)
А3. $ нулевой элемент θ, обладающий свойствами α+θ=α для " α Î F
А4. $ противоположный элемент (–α): α+(-α)=θ для " α Î F
B1. α*β =β*α для " α,β Î F
B2. (α*β)*γ=α*(β*γ) для " α,β,γ Î F
B3. $ единичный элемент 1 Î F 1*α =α для " α Î F, 1≠θ
B4. $ обратный элемент (α-1) Î F: α*α-1 = 1 для " α Î F, α≠θ
C1. α*(β+γ)=α*β+α*γ для " α,β,γ Î F (дистрибутивность умножения относительно сложения)
Операции сложения и умножения для элементов поля являются алгебраическими, т.е. являются бинарными, однозначными и замкнутыми.
Следствия из аксиом поля:
1. В F $ единственный нулевой элемент θ
2. Для " α Î F $ единственный противоположный элемент (-α)
3. α+(-β)=α-β (определение вычитания). Вычитание обратно сложению.
4. -(α+β)=(-α)+(-β)
5. В F $ единственный единичный элемент.
6. Для " α Î F (α≠θ) $ единственный обратный элемент α-1
7. (α*β)-1=α-1*β-1 (α≠θ, β≠θ)
8. α*β-1 = α/β (определение деления)
9. θ*α = θ для " α Î F
10. –α = (-1)*α
Примеры полей:
Поле вещественных чисел R, поле комплексных чисел C, поле рациональных чисел. Примечание: целые числа не образуют поля, т.к. при делении выходим из мн-ва.
Комплексным числом z называется упорядоченная пара z=(a,b) действительных чисел со следующими св-вами:
10. Два комплексных числа z1=(a1,b1) и z2=(a2,b2) равны тогда и только тогда, когда a1= a2 и b1= b2.
20.Сумма двух комплексных чисел z1=(a1,b1) и z2=(a2,b2) определяется след. образом: z1+ z2=(a1,b1)+(a2,b2)=( a1+a2,b1+b2).
30. Вычитание двух комплексных чисел z1=(a1,b1) и z2=(a2,b2) определяется как операция, обратная сложению: z1–z2=(a1,b1)-(a2,b2)=(a1-a2,b1-b2).
40. Произведение двух комплексных чисел z1=(a1,b1) и z2=(a2,b2) определяется след. образом: z1z2=(a1,b1)(a2,b2)=( a1a2-b1b2, a1b2+ a2b1).
50. Деление двух комплексных чисел z1=(a1,b1) и z2=(a2,b2) определяется как операция, обратная произведению: z1/z2=(a1,b1)/(a2,b2)=((a1a2+b1b2)/(a22+b22),(a2b1-a1b2)/(a22+b22)), при a22+b22≠0.
Алгебраическая форма записи комплексного
числа: i=(0,1)(i – мнимая единица), ¶=(1,0)(¶ - единичный вектор) z=(a,b)=(a,0)+(0,b)=a(1,0)+b(0,1)=a+ib; а – действительная
часть комплексного числа z(Re z), b – мнимая часть
комплексного числа z(Im z). Тригонометрическая форма записи комплексного числа: z=a+ib получается при
использовании связи декартовых и полярных координат (a=r cosφ, b=r sinφ), т.е. z=r(cosφ+i sinφ). При этом полярный радиус r называется модулем комплексного числа z (обознач. |z|), полярный угол φ –
аргументом комплексного числа z (обознач. Arg z). Модуль и аргумент
комплексного числа выражается через его действительную и мнимую части след образом:
r=|z|=![]() ; cosφ=a/
; cosφ=a/![]() ; sinφ=b/
; sinφ=b/![]() .
.
Главным значением аргумента комплексного числа (обознач. arg z) считают такой его аргумент φ, что –π<φ≤π, если z≠0, и φ=0, если z=0. arg z=arct b/a, если a>0;=arctg b/a+π, если a<0, b>0;=arctg b/a-π, если a<0, b<0.
Arg z=arg z+2kπ, kÎZ. z1z2=r1r2(cos(φ1+φ2)+isin(φ1+φ2)); z1/z2=r1/r2(cos(φ1-φ2)+isin(φ1-φ2)).
![]() =(a,-b)=a-ib – комплексно-сопряженное
с z число. 1.
=(a,-b)=a-ib – комплексно-сопряженное
с z число. 1.![]()
2.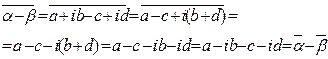
3.![]()
4.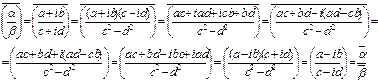
5.![]()
Матрицы. Действия с ними.
Def: Совокупность чисел αij Î F, расположенных в виде таблицы размера mxn называется матрицей.
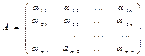 , если m=n то
матрицу называют квадратной порядка m
, если m=n то
матрицу называют квадратной порядка m
Матрицы А, В считаются равными, если αij=βij. ![]() ,
,![]() . Матрица В называется произведением
матрицы A на λ, если каждый элемент Î B получен путем умножения каждого элемента матрицы А на λ.
. Матрица В называется произведением
матрицы A на λ, если каждый элемент Î B получен путем умножения каждого элемента матрицы А на λ.
Свойства матриц.
1. 1*A= A
2. θ*A= 0 (нулевой матрице)
3. λ*(μ*A)=(λ*μ)*A для " λ, μ Î F
Def: Пусть А,В,С – матрицы одинаковых размеров. C=(γij) называется суммой А и В, если
выполняется условие γij=αij+βij ![]() ,
,![]() .
.
Свойства:
1. А+В=В+А
2. А+(В+С)=(А+В)+С
3. (А+0)=А (0-нулевая матрица)
4. -1*А= -А А+(-А)=0
5. (λ+μ)*A=λ*A+μ*A
6. λ*(A+B)=λ*A+λ*B
7. A+A=2*A
8. (–λ)*A=-(λ*A) -(A+B)=-A-B -(-A)=A
Def: Пусть есть матрица А, у которой m строк и n столбцов, и матрица В, у которой n строк и k столбцов. Для того, чтобы можно было умножать, надо чтобы число столбцов первой матрицы совпадало с числом строк второй.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.