Аmxn*Bnxk=Cmxk
Свойства:
1. А*В=В*А
2. А*(В*С)=(А*В)*С
3. (A+B)*C=A*C+B*C
4. C*(A+B)=C*A+C*B
5. λ*(A*B)=(λ*A)*B=A*(λ*B)
Любые квадратные матрицы порядка n можно складывать, умножать и умножать на число.
Def: Квадратная матрица А называется диагональной,
если все ее недиагональные элементы равны нулю, т.е. 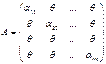 .
Сумма и произведение диагональных матриц – снова диагональная матрица.
.
Сумма и произведение диагональных матриц – снова диагональная матрица.
Def: Диагональная матрица с диагональными элементами равными единице, называется единичной и обозначается I (или E).
А*I=A=I*A
Определение и простейшие свойства определителей.
Пусть
дана квадратная матрица А, состоящая из n строк и n
столбцов. Рассмотрим всевозможные произведения n элементов
матрицы, взятых по одному из каждой строки и каждого столбца. В силу того, что αij Î F, в котором операция умножения коммутативна, мы можем
упорядочить сомножители по номерам столбцов; в результате получим произведение
вида ![]() , в котором i1,…,in – номера строк после перестановки сомножителей.
Очевидно, что i1,…,in – некоторые
перестановки чисел 1,2,..,n. Условимся брать произведение 1 со знаком «+» или «-»
в зависимости от четности или нечетности числа инверсий последовательности i1,…,in.
, в котором i1,…,in – номера строк после перестановки сомножителей.
Очевидно, что i1,…,in – некоторые
перестановки чисел 1,2,..,n. Условимся брать произведение 1 со знаком «+» или «-»
в зависимости от четности или нечетности числа инверсий последовательности i1,…,in.
Def: Инверсией (беспорядком) последовательности i1,…,in называют такое расположение индексов, при котором старший индекс стоит впереди младших. Число всех беспорядков последовательности обозначается N(i1,…,in).
Def: Определителем матрицы А называется сумма всевозможных произведений вида 1 со знаком (-1)N(i1,…,in).
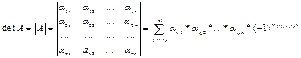
Будем считать положительным
направлением для строк: слева направо, для столбцов: сверху вниз. Отрезки,
соединяющие два каких-либо элемента матрицы, так же могут указывать
направление. А именно, будем говорить, что отрезок, соединяющий элемент αij с αkl имеет положительный наклон, если его
правый конец расположен ниже левого, и отрицательный наклон, если его правый
конец выше, чем левый. Мысленно проведем все отрезки, соединяющие попарно ![]() (1), имеющие отрицательный наклон. Ставим знак «+», если
число таких отрезков четно, и знак «-» в противном случае.
(1), имеющие отрицательный наклон. Ставим знак «+», если
число таких отрезков четно, и знак «-» в противном случае.
Свойства определителей:
Def: 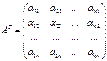 ,
полученная из
,
полученная из 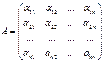 заменой строк на столбцы с теми
же номерами, называется транспонированной по отношению к матрице А.
заменой строк на столбцы с теми
же номерами, называется транспонированной по отношению к матрице А.
1. detA=detAT. Оба определителя состоят из одних и тех же членов, поэтому нам достаточно доказать что одинаковые члены в определителях матриц А и АТ имеют одинаковые знаки. Очевидно, что транспонирование квадратной матрицы сводится к ее повороту на 180 градусов вокруг диагонали. Каждый отрезок с отрицательным наклоном переходит в отрезок с отрицательным наклоном, поэтому число отрезков с отрицательным наклоном, соединяющих элементы данного члена после транспонирования не изменятся. Следовательно, не изменится и знак этого члена. Поскольку знаки всех членов сохранятся, величина определителя останется прежней. Рассмотренное свойство устанавливает равноправие его строк и столбцов. Поэтому дальнейшие свойства определителей будем формулировать и доказывать только для столбцов. При этом следует помнить, что для строк они также будут иметь место.
2. Антисимметрия столбцов: под антисимметрией столбцов понимают свойство определителя менять свой знак при перестановке двух столбцов.
3. Определитель, имеющий два одинаковых столбца равен нулю. Переставляя эти одинаковые столбцы, мы не изменим определитель, но с другой стороны, по свойству 2 он должен изменить свой знак.
4.
Линейное свойство определителя.
Если все элементы j-го столбца определителя D представимы в
виде αij=λ*βi+ μ*γi для всех i=1..n, то определитель
D=λ*D1+ μ*D2. Причем у определителей D1 и D2 все
столбцы, кроме i-го и j-го такие же, как у определителя D,а i-ый
столбец в определителе D1 состоит из чисел βi, а D2 – γi 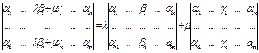
5. Общий множитель всех элементов некоторого столбца можно вынести за знак определителя. Dj(αij)=Dj(λ βi)=λ Dj(βi)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.