Поля. Алгебраические операции для элементов поля. Комплексное число. Алгебраическая форма записи комплексного числа, страница 11

||x+y|| <= ||x|| + ||y||

Теорема: Всякое Евклидово пространство является нормированным, если в нем норму "x определить равенством: ||x|| = 

Доказательство: Покажем, что для нормы определенной в соотношении справедливы аксиомы 1-3 определения нормированного пространства.

1)  ||x||>0

Справедливость сразу вытекает из аксиомы 4 скалярного произведения

2)  ||λx|| =  =  = |λ| следует из 1 и 2 аксиом скалярн. произвед.

3)  ||x+y|| = = <= = ||x|| + ||y||

Углом j между векторами  x,yÎE называется угол, косинус которого определен выражением: cosj =

Ортонормирванный базис и его свойства.

Def: Два ненулевых вектора х и у  называются ортогональными, если угол между ними равен , т.е.   если их скалярное произведение равно 0.

Теорема Пифагора: Если х и у Î E ортогональны, то квадрат норм ||x+y||²= ||x||²+||y||².

Def: В Евклидовом пространстве особую роль играют ортонормированные базисы. Будем говорить, что e₁,e₂,…,e_n Î E образуют ортонормирован  ный базис, если эти элементы попарно ортогональны и норма каждого из векторов равна 1.

 - дельта Кронекера.

Теорема 3: во всяком n-мерном Евклидовом пространстве Е $ ортонормированный базис.

Свойства ортонормированного базиса:

Пусть e1,e2,…,en – произвольный ортонормированный базис пространства Е, а х и у – два произвольных вектора этого пространства. Найдем выражение х и у через координаты х и у в базисе e1…en

      

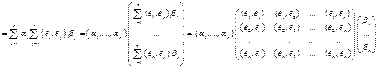                                Матрица скалярных произведений – матрица Грамма.

В ортонормированном базисе скалярное произведение двух " векторов = сумма произведений координат этих векторов.

Координаты произвольного вектора относительно ортонормированного базиса равны скалярному произведению этого вектора на соответствующие базисные векторы. Эти произведения можно назвать проекциями вектора х ан соответствующие базисные векторы.

Теорема: ортогональн. сумма ненулевых подпр-в явл. прямой суммой.

Д-во: Если L₁ и L₂ – подпр-ва пр-ва Е, L₁┴L₂ и zÎ(L₁∩L₂), то (z,z)=0, т.к. zÎL₁ и zÎL₂. Отсюда следует, что z=0, и потому L₁∩L₂={0}. Ввиду признака прямой суммы получаем требуемый рез-т.

Разложение Евклидова пространства на ортогональную(прямую) сумму своего подпространства и его ортогонального дополнения.

Def: Два множества F и G векторов евклидова пространства Е называются  ортогональными, если каждый вектор из F ортогонален каждому вектору из G.

Лемма 1: Для того, чтобы вектор х был ортогонален к подпространству L, необходимо и достаточно, чтобы он был ортогонален всем векторам какого-либо базиса L.

Следствие 1: Для того, чтобы два подпространства были ортогональны, необходимо и достаточно, чтобы каждый вектор какого-либо базиса одного подпространства был ортогонален всем векторам какого-либо базиса другого подпространства.

Def: Сумма подпространств L=L₁+…+L_n называется ортогональной суммой, если подпространства, образующие ее попарно ортогональны. Обозначается

Лемма 2: Ортогональная сумма ненулевых подпространств всегда является прямой суммой.

Def: Совокупность всех векторов ортогональных некоторому непустому множеству F векторов Евклидова Пространства Е называется ортогональным дополнением множества F и обозначается . Она является подпространством

Теорема 4: Евклидово пространство есть ортогональная сумма любого своего подпространства L и его ортогонального дополнения.

Доказательство: Пусть размерность L равна s, а размерность  равна m. Выберем ортонормированный базис e₁,…,e_S подпространства L и ортонормированный базис f₁,…,f_m для . Система векторов e₁,…,e_S,f₁,…,f_m является ортонормированной между собой и линейно независимой. Если эта система не является базисом Е, то ее можно дополнить до ортонормированного базиса Е. Пусть g – один из таких дополнительных векторов. Поскольку g ортогонален e_i, то g Î L, но g ортогонален и f_i, значит g Î , значит . Но пересечение этих пространств возможно только по нулевому вектору, значит g – нулевой вектор и система базисов полна.

Лемма 3: Если в ЕП Е задана некоторая система векторов и единственным вектором из Е, ортогональным к этим векторам, является нулевой, то ранг системы равен размерности Е.