Перпендикуляр, проекция, наклонная. Изоморфизм.
Пусть хÎЕ, gÎL, h Î
. Найдем g и h. То есть, x – наклонная, g – проекция, h –
перпендикуляр. Выберем e1,…,em – базис L. x=g+h, g=α1e1+…+αmem. Воспользуемся тем, что hÎ
:
(h, ei)=(x- α1e1-…-αmem, ei)=(x,ei)-α1(e1,ei)-…-αm(em,ei)=0. для " i=1..m
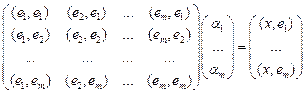
Изоморфизм n-мерных ЕП.
Def: Два ЕП Е и Е’ называются изоморфными если между векторами этих пространств можно установить взаимнооднозначное соответствие так, что если между векторами х и у Î Е отвечают соответствующие векторы x’, y’ Î E’, то вектору х+у Î Е отвечает вектор x’+y’ Î E’, а вектору λx Î Е отвечает вектор λx’ Î Е’ и скалярное произведение (x, y)=(x’, y’); Таким образом евклидовы пространства изоморфны, если они изоморфны, как линейные пространства и если этот изоморфизм сохраняет величину скалярного произведения этих пар векторов.
Теорема 5: Все евклидовы пространства одной и той же размерности изоморфны между собой.
Д-во: возьмем 2 произвольных E и Е’ одинаков. размерности. Они изоморфны как лин. пр-ва. Выберем ортонорм. базисы e1,…,en и e’1,…,e’n в пр-вах E и Е’ соответственно. Тогда для люб. век-ов x и y: x=α1e1+…+αnen; y=β1e1+…+βnen; поставим в соотв. x<->x’: x’=α1e’1+…+αne’n; а у<->y’: y’=β1e’1+…+βne’n. Тогда скалярн. произвед. (x,y)=(x’,y’).
Замечание: Если в каком-либо конкретном n-мерном Евклидовом пространстве E’ доказана теорема, сформулированная в терминах операций сложения векторов, умножения векторов на числа и скалярного произведения, то эта теорема справедлива и в совершенно произвольном n-мерном Евклидовом пространстве Е.
Унитарное пространство. Неравенство Коши-Буняковского
Def: Комплексное линейное пространство U называется унитарным, если каждой паре векторов x,y Î U поставлены в соответствие комплексное число (x,y)ÎC, называемое скалярным произведением. Причем выполнены следующие аксиомы.
1. 
2. 
3. (x+y,z)=(x,z)+(y,z)
4. (x,x) есть вещественное
неотрицательное число, равное нулю тогда и только тогда, когда 
. (x,x)≥0
I. (ix,ix)=(0,i2x2)=(0,-x2)
II. (ix,ix)=i2(x,x)=-1(x,x)
Следствия из аксиом скалярного произведения
1. 
2. 
Пример: пространство Сn является унитарным пространством.
Неравенство Коши-Буняковского.
|(x,y)|2≤(x,x)(y,y)
Доказательство.
Рассм.
;
Что и требовалось доказать.
Заметим, что угол между векторами x,y Î U не определен, т.к. cos – функция, определенная над полем вещественных чисел, а скалярное произведение в U – есть величина комплексная, однако понятие ортогональности векторов остается.
Доказать, что в любом унитарном(комплексном) пространстве существует ортонормированный базис. Свойства ортонормированного базиса.
Def: Ортонормированным базисом n-мерного унитарного пространства называется совокупность векторов e1,…,en, удовлетворяющих соотношениям 
Можно показать, что
ортогональные векторы линейно-независимы в U. Также устанавливается существование в произвольном n-мерном унитарном пространстве ортонормированного
базиса.
Как и в случае вещественного пространства координаты произвольного вектора х относительно ортонормированного базиса равны скалярным произведениям этого вектора на соответствующие базисные векторы. Также можно доказать, что все унитарные пространства одной размерности изоморфны между собой.
Процесс ортогонализации Грамма-Шмидта: от люб. л/н сист. век-ов x1,…,xm евкл. пр-ва можно перейти к ортогональной сист. y1,…,ym, состоящей из ненулевых векторов. Такой переход совершается с помощью процесса ортогонализации Грамма-Шмидта по след. формулам: y1=x1; y2=x2+α21y1, α21=-(x2,y1)/(y1,y1); y3=x3+α31y1+α32y2, α31=-(x3,y1)/(y1,y1), α32=-(x3,y2)/(y2,y2); ym=xm+αm1y1+αm2y2+…+αm,m-1ym-1, αmi=-(xm,yi)/(yi,yi), i=1,…,m-1. Если процесс ортогонализации применять к л/з сист. век., то на некотором шаге обязательно получится нулевой вектор. Пусть e1,…,em – ортонорм. базис n-мерного евкл. пр-ва L и для век-ов x,yÎL имеют место разложения x=α1e1+…+αnen; y=β1e1+…+βnen; В этом случ. справедливы рав-ва: (x,y)= α1β1+…+αnβn; (x,x)=α12+…+αn2; αi=(x,ei), βi=(y,ei), i=1,…,n.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.