Собственные векторы и собственные значения

Собственные векторы и собственные значения

В дальнейшем особую роль будут играть одномерные инвариантные подпространства.

Пусть  – одномерное подпространство, порожденное ненулевым вектором . Ясно, что для того чтобы  было инвариантно, необходимо и достаточно, чтобы выполнялось условие

                                      .                                                    (1)

Определение. Вектор , удовлетворяющий соотношению (1), называется собственным вектором, а соответствующее число λ – собственным значением (характеристическим числом) линейного оператора A.

Таким образом, если x – собственный вектор, то векторы ax образуют одномерное инвариантное подпространство. Обратно, все отличные от нуля векторы одномерного инвариантного подпространства являются собственными.

Теорема 1. В комплексном линейном пространстве X всякий линейный оператор A имеет хотя бы один собственный вектор.

Доказательство. Пусть в X выбран базис , в этом базисе линейному оператору A соответствует матрица с элементами 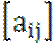.Выберем произвольный вектор . Тогда

  

и координаты  вектора  выражаются формулами

, .

Отсюда условие того, что x – собственный вектор () записывается в виде

,

или

                  (2)

Для доказательства теоремы нужно установить существование числа λ и чисел  (не всех равных нулю), удовлетворяющих системе (2).

Условием существования ненулевого решения однородной системы (2) является равенство нулю ее определителя

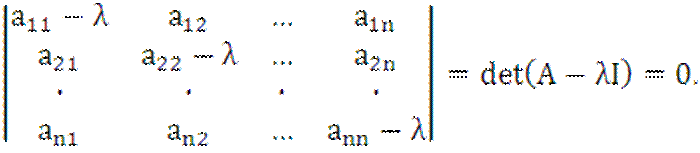                 (3)

Мы получили уравнение n-ой степени относительно λ. Это уравнение имеет хотя бы один (в общем случае комплексный) корень .

Подставив в систему (2) вместо λ корень , мы получим однородную СЛАУ с нулевым определителем, имеющую ненулевое решение .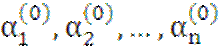

Тогда вектор

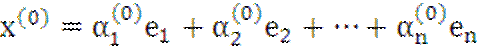
будет собственным вектором, отвечающим собственному значению .

Определение. Многочлен, стоящий в левой части уравнения 3 называется характеристическим многочленом матрицы оператора A, а само уравнение (3) характеристическим или вековым уравнением этой матрицы.

Доказывая теорему 1, мы установим, что собственные значения оператора A являются корнями характеристического многочлена.

Теорема 2. Характеристический многочлен не зависит от выбора базиса.

Доказательство. Зафиксируем в пространстве X некоторый базис  и обозначим через  матрицу оператора A в этом базисе. Пусть в некотором базисе  оператор A имеет матрицу . Тогда

,

где P – матрица преобразования координат при переходе от базиса  к базису .

                          

Вычисление собственных векторов линейного оператора требует знания собственных значений. Для этого в общем случае приходится решать характеристическое уравнение.

Если матрица оператора A треугольная, т.е. имеет вид

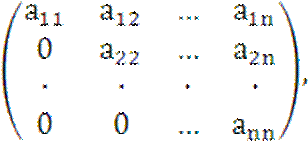                                                                  (4)

то собственные значения находятся непосредственно – ими будут числа, стоящие на диагонали, т.е. .

Простейшие линейные операторы имеют n () линейно независимых собственных векторов. Пусть A – такой линейный оператор, а  - его линейно независимые собственные векторы, т.е.

, .

Выберем  в качестве базиса линейного пространства X. В этом базисе матрица оператора A будет диагональной, т.е.

.

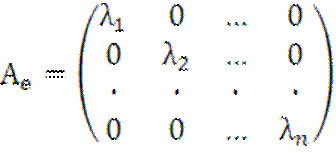Отсюда вытекает

Теорема 3. Если линейный оператор A имеет n линейно независимых собственных векторов (является оператором простой структуры), то, выбрав их в качестве базиса линейного пространства, мы приведем матрицу линейного оператора A к диагональной форме. Обратно, если в некотором базисе матрица линейного оператора диагональна, то все векторы этого базиса являются собственными векторами.

Теорема 4. Система собственных векторов , соответствующая попарно различным собственным значениям , линейно независима.

Доказательство. Воспользуемся методом математической индукции.

Пусть n=1. Поскольку , теорема верна.

Пусть теорема верна для (n-1) векторов, докажем ее для n векторов. Предположим противное, т.е. что

                        ,                               (6)

причем хотя бы один из коэффициентов , например .

Подействуем на обе части равенства (6) оператором A. Получим:

 .

Вычитая из последнего равенства равенство (6),умноженное на , и получим:

,

где первый коэффициент  по-прежнему отличен от нуля. Последнее противоречит индуктивному предположению о линейной независимости векторов .

Теорема 5. Если характеристический многочлен оператора A имеет n различных корней, то матрица оператора A может быть приведена к диагональной форме.

Доказательство. Каждому корню  отвечает хотя бы один собственный вектор. Т.к. соответствующие этим векторам собственные значения различны, согласно теореме 4 мы имеем n линейно независимых собственных векторов . Если векторы принять за базис, то матрица оператора A будет диагональной.

Теорема 6. Собственные векторы линейного оператора, соответствующие одному собственному значению λ, вместе с нулевым вектором образуют подпространство пространства X.

Доказательство. Пусть  и  – два собственных вектора, отвечающие одному собственному значению λ. Тогда

   ,

т.е.  также является собственным вектором, соответствующим собственному значению λ. Указанное подпространство совпадает с ядром оператора .