Евклидово пространство
Аксиоматически введем скалярное произведение векторов в вещественном пространстве.
Определение.
Будем говорить, что в вещественном пространстве L
определено скалярное произведение, если каждой паре векторов х, у
![]() L поставлено в
соответствие действительное число, обозначаемое (х, у). При этом выполняются
следующие аксиомы:
L поставлено в
соответствие действительное число, обозначаемое (х, у). При этом выполняются
следующие аксиомы:
1° (х, у)=(у, х) – симметричность;
2° (λх, у)=λ(х,
у), λ![]() R;
R;
3° (х + у, z)=(х, z) + (у, z) – дистрибутивность;
4° (х, х) >
0, если х ![]() , (х, х)=0, если х =
, (х, х)=0, если х =![]() .
.
Следствия их аксиом скалярного произведения:
а) (х, λу) = λ (х, у);
б) (х, у + z)=(х, у) + (х, z).
Определение. Линейное пространство L со введенным скалярным произведением называется евклидовым пространством и обозначается Е.
Здесь мы не уточняем природу элементов линейного пространства L, правила образования х + у, λх и скалярное произведение. Важно, чтобы эти правила удовлетворяли аксиомам линейного пространства и аксиомам 1° - 4° скалярного произведения.
Примеры евклидовых пространств
1. Пространство V3. (х, у)=|х||у|cos(х, у).
2. Пространство Rn.
х=![]() , у=
, у=![]() ;
;
х + у=![]() , λх=
, λх=![]() , (х, у)=
, (х, у)=![]() .
.
Можно показать, что аксиомы 1° - 4° выполняются.
3. В произвольном n - мерном линейном пространстве L, заданном
над полем вещественных чисел, выберем базис е1, е2, …, еn. Тогда ![]() х, у
х, у![]() L х=
L х=![]() , у=
, у=![]() и
скалярное произведение можно ввести несколькими способами:
и
скалярное произведение можно ввести несколькими способами:
а) (х, у)=![]() ;
;
б) (х, у)=![]() (
λ1, λ2, …, λn –
фиксированные положительные числа);
(
λ1, λ2, …, λn –
фиксированные положительные числа);
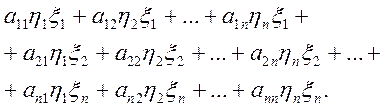 в)
(х,у)=хтАу=
в)
(х,у)=хтАу=![]()
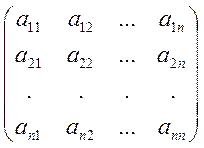
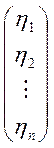 =
=
=
Аксиомы 2° и 3° выполняются при любой квадратной матрице А nхn.
Аксиома 1°
выполняется, если aij=aji ![]() i, j (А = Ат).
i, j (А = Ат).
Аксиома 4°
требует, чтобы хтАх>0 ![]() х
х![]() ,
т.е. А должна быть положительно определенной (А>0)
,
т.е. А должна быть положительно определенной (А>0)
Простейшие свойства евклидова пространства.
Теорема 1. Для любых двух векторов х и у произвольного евклидова пространства Е справедливо неравенство Коши – Буняковского (– Шварца):
(х,
у)2![]() (х, х)(у, у).
(х, х)(у, у).
Доказательство.
Для![]() в силу аксиомы 4° скалярного произведения
в силу аксиомы 4° скалярного произведения
(![]() х - у,
х - у, ![]() х - у)
х - у) ![]() 0.
0.
В силу аксиом 1° - 3°, последнее неравенство можно записать в виде
(![]() х - у,
х - у, ![]() х - у)=(
х - у)=(![]() х,
х, ![]() х - у) -
(у,
х - у) -
(у, ![]() х - у) =
х - у) =
=(![]() х,
х, ![]() х) - (
х) - (![]() х, у) - (у,
х, у) - (у, ![]() х) + (у,
у) =
х) + (у,
у) =
=![]() 2(х, х) -
2(х, х) - ![]() (х, у) -
(х, у) - ![]() (у, х) +
(у, у) =
(у, х) +
(у, у) =
=![]() 2(х, х) -
2(х, х) - ![]() (х, у) -
(х, у) - ![]() (х, у) +
(у, у) =
(х, у) +
(у, у) =
= ![]() 2 (х, х) - 2
2 (х, х) - 2 ![]() (х, у) + (у, у)
(х, у) + (у, у) ![]() 0.
0.
Полученный квадратный трехчлен принимает неотрицательные значения, если и только если его дискриминант
b2 - 4ac=4(х, у)2
- 4(х, х)(у, у) ![]() 0.
0.
Следовательно,
(х,
у)2![]() (х, х)(у, у).
(х, х)(у, у).
Теорема 1а. Неравенство Коши – Буняковского обращается в равенство тогда и только тогда, когда векторы х и у коллинеарны.
Доказательство.
Достаточность. Пусть х и у коллинеарны, т.е. х =![]() у. Тогда
у. Тогда
(х, у)2=(![]() у, у) 2=
у, у) 2=![]() 2
(у, у) 2
2
(у, у) 2
и
(х, х)(у, у)=(![]() у,
у, ![]() у)(у, у)=
у)(у, у)=![]() 2 (у, у) 2 .
2 (у, у) 2 .
Т.е. в неравенстве Коши – Буняковского имеет место равенство.
Необходимость. Пусть теперь для некоторых х, у
(х, у)2 = (х, х)(у, у).
Если у=![]() , то векторы коллинеарны. Если же у
, то векторы коллинеарны. Если же у![]()
![]() , то выберем
, то выберем ![]() =
=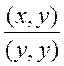 .Тогда
.Тогда
(х - ![]() у, х -
у, х - ![]() у)=(х, х)
-
у)=(х, х)
- ![]() (х, у) -
(х, у) - ![]() (у, х) +
(у, х) +
![]() 2(у, у)=
2(у, у)=
=(х, х) - 2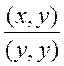 (х, у) +
(х, у) + 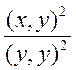 (у, у)=(х,
х) -
(у, у)=(х,
х) - 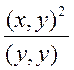 =(х, х) - (х, х)=0,
=(х, х) - (х, х)=0,
т.е х - ![]() у=0 и х =
у=0 и х =![]() у.
у.
Введем в произвольном евклидовом пространстве понятие нормы (или длины) каждого вектора.
Определение.
Линейное пространство L называется нормированным,
если каждому вектору х![]() L
ставится в соответствие вещественное число ||х||, называемое нормой
(или длиной) х и при этом выполняются следующие три аксиомы:
L
ставится в соответствие вещественное число ||х||, называемое нормой
(или длиной) х и при этом выполняются следующие три аксиомы:
1°. ||х||>0,
если х![]()
![]() , ||х||=0, если х=
, ||х||=0, если х=![]() ;
;
2°. ||![]() х||=|
х||=|![]() |||х||
|||х|| ![]() ,
,![]() ;
;
3°. ![]() справедливо неравенство
справедливо неравенство
||х+у||![]() ||х||+||у||,
||х||+||у||,
называемое неравенством треугольника (или неравенством Минковского).
Теорема 2. Всякое евклидово пространство является нормированным, если в нем норму любого вектора х определить равенством
||х|| =![]() .
.
Доказательство. Нужно показать, что для нормы, определенной предыдущим соотношением, справедливы аксиомы 1°-3° определения нормированного пространства. Справедливость аксиомы 1° сразу вытекает из аксиомы 4° скалярного произведения. Справедливость аксиомы 2° следует из аксиом 1° и 2° скалярного произведения. Убедимся в справедливости аксиомы 3°. Запишем неравенство Коши – Буняковского
|(х, у)|![]()
![]() .
.
С помощью аксиом 1°-4° скалярного произведения и определения нормы отсюда получим
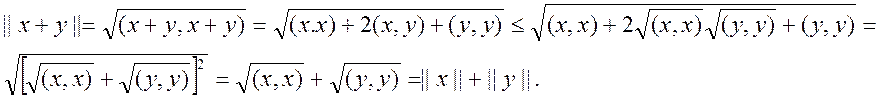
Пример:
Пусть L – n-мерное вещественное линейное пространство, е1, е2, …, еn – базис в L.
![]() или хт=
или хт=![]() ,
,
![]() или ут=
или ут=![]() .
.
(х,у)=хтАу=![]()
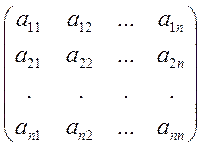
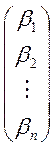 =
=
=![]()
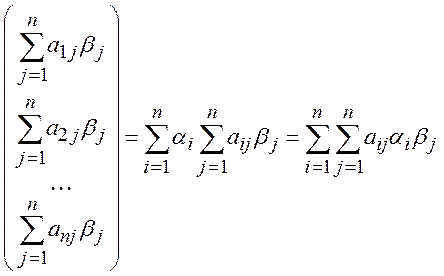
Проверим выполнение аксиом скалярного произведения
1°. (у,х)= утАх=(утАх)т=хтАту;
(х,у) = (у,х) ![]() А=Ат, т.е. А – симметричная
матрица.
А=Ат, т.е. А – симметричная
матрица.
2°. ![]() =(
=(![]() х)тАу=(
х)тАу=(![]() хт)Ау=
хт)Ау=![]() (хтАу)=
(хтАу)= ![]() (х,у).
(х,у).
3°. (х+у,z)=(x+y)тАz=(хт+ут)Аz=хтАz+утАz=(х,z)+(y,z).
4°. (х,х)= хтАх>0
при х![]() , т.е. А – положительно определенная
матрица
, т.е. А – положительно определенная
матрица
В любом вещественном евклидовом пространстве можно ввести понятие угла между двумя произвольными векторами х и у этого пространства.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.