Евклидово пространство. Простейшие свойства евклидова пространства. Свойства ортонормированного базиса, страница 3

Доказательство. Пусть е₁,е₂,…, е_k – базис L. Если хL, то х ортогонален ко всем векторам из L и, в частности, к векторам е₁,е₂,…, е_k.

Обратно. Пусть (х,e_i)=0 . i=1,2,…,k. Возьмем произвольный вектор zL, z =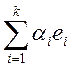. Тогда

(х,z)= .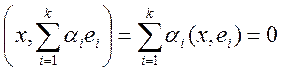

Следствие. Для того чтобы два подпространства были ортогональны, необходимо и достаточно, чтобы каждый вектор какого-либо базиса одного подпространства был ортогонален ко всем векторам какого-либо базиса другого подпространства.

Определение Сумма подпространств

L=L₁+L₂+…+L_m

называется ортогональной, если подпространства, образующие её, попарно ортогональны. Ортогональную сумму будем обозначать так:

L=L₁L₂…L_m.

Лемма 2. Ортогональная сумма ненулевых подпространств всегда является прямой суммой.

Доказательство. Выберем в каждом подпространстве ортонормированный базис и рассмотрим систему векторов, представляющую собой объединение базисов всех подпространств. Любой  вектор из ортогональной суммы линейно выражается через векторы построенной системы. Но эта система линейно независима, Т.к. состоит из ненулевых попарно ортогональных векторов. Утверждение леммы вытекает из теоремы о том, что L – прямая сумма L₁,…, L_m тогда и только тогда, когда объединение базисов L₁,…, L_m дает базис  L.

Определение Совокупность всех векторов, ортогональных некоторому непустому множеству F векторов евклидова пространства E, называется ортогональным дополнением множества F и обозначается F.

Ортогональное дополнение есть подпространство. Действительно, если х,у F, то х,уF. Но тогда F R, т.е.  F.

Теорема 4 Евклидово пространство E есть ортогональная сумма любого своего линейного подпространства L и его ортогонального дополнения L, т.е.

Е= L L.

Доказательство Пусть dim L=s, dim L=m. Выберем ортонормированный базис е₁,е₂,…, е_s подпространства L и ортонормированный базис f₁,f₂,…, f_m подпространства L. Система векторов е₁,…, е_s, f₁,…, f_m – ортонормированная и, следовательно, линейно независимая. Если эта система не является базисом Е, то ее можно дополнить до ортонормированного базиса Е. Пусть g– один из дополнительных векторов. Он ортогонален к е₁,е₂,…, е_s, Т.е. gL. Но, с другой стороны, g ортогонален к f₁,f₂,…, f_m, поэтому gL. Т.о., gLи gL. Значит, g =, что и доказывает теорему 4.

Лемма 3 Если в евклидовом пространстве Е задана некоторая система векторов х₁,х₂,…, х_k и единственным вектором из Е, ортогональным к этим векторам, является нулевой вектор, то ранг системы равен размерности Е.

Доказательство Обозначим через L=L(х₁,х₂,…, х_k) линейную оболочку системы векторов х₁,х₂,…, х_k. Любой вектор, ортогональный к данным векторам, принадлежит ортогональному дополнению L. По условию леммы, L состоит только из нулевого вектора. Учитывая, что Е= L L, отсюда получаем, что dim L = dim Е. Поскольку dim L равна рангу системы векторов х₁,х₂,…, х_k, лемма доказана.

Перпендикуляр, проекция, наклонная.

L – подпространство евклидова пространства Е

x

h

х –наклонная к L, хЕ.

L

g- проекция х на подпространство L , gL

g

h – перпендикуляр, опущенный из х наL, h L

Разложение

х=g+h

будет единственным. Найдем g и h. Выберем е₁,е₂,…, е_m – базис в L. Тогда

g=. Известно, что

h=x-gе_i .

Отсюда

(х---…-,) = 0

или

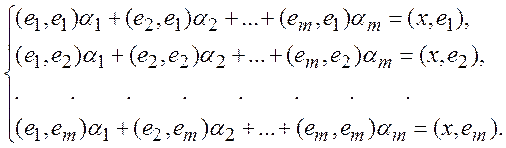
Разрешив систему

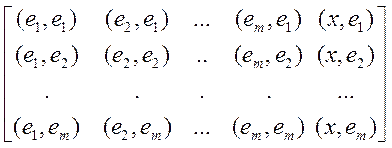
относительно , найдем проекцию g, а затем и перпендикуляр h.

Изоморфизм n-мерных евклидовых пространств

Определение Два евклидовых пространства Е и Е^’ называются изоморфными, если между векторами этих пространств можно установить  взаимно однозначное соответствие так, что если векторам х и у пространства Е отвечают соответственно векторы х^’ и у^’ пространства Е^’, то вектору х+у из Е отвечает х^’+у^’ из Е^’, вектору х из Е отвечает х^’ из Е^’ и скалярное произведение (х,у) равно скалярному произведению (х^’,у^’).

Т.о., евклидовы пространства  Е и Е^’ изоморфны, если они изоморфны как линейные пространства и если этот изоморфизм сохраняет величину скалярного произведения соответствующих пар векторов.

Теорема евклидова изоморфизма. Все евклидовы пространства одной и той же рахмерности изоморфны между собой.

Доказательство Возьмем два произвольных евклидовых пространства Е и Е^’ одинаковой размерности. Они изоморфны как линейные пространства. Выберем ортонормированные базисы е₁,е₂,…, е_n  и е^’₁,е^’₂,…, е^’_n в Е и Е^’ соответственно. Тогда х,уЕ

х=, у=

Поставим х и у в соответствие х^’,у^’Е^’. При этом

х^’=, у=

и (х,у)= =(х^’,у^’).

Т.о., если в каком-либо конкретном n-мерном евклидовом пространстве Е^’ доказана теорема, сформулированная в терминах операций сложения, умножения на числа и скалярного произведения, то эта теорема справедлива и в совершенно произвольном n-мерном евклидовом пространстве Е.