Министерство Образования Российской Федерации
Новосибирский Государственный Технический Университет
Кафедра Прикладной Математики
Задание по Геометрии и алгебре
на тему «Евклидовы пространства»
Факультет: ПМИ
Группа: ПМ-63
Студент: Тишков И.В.
Вариант: 21
Преподаватель: Бобылева Д.И.
Новосибирск 2006
Выпишем векторы, которые образуют подпространство L. Пусть это будут векторы:
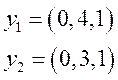
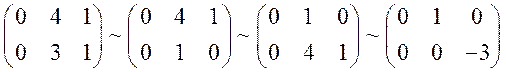
Наклонная (заданный вектор x) определим, как:
![]()
Мы
знаем, что трехмерное пространство ![]() единственным образом представимо в виде суммы
единственным образом представимо в виде суммы ![]() и
и ![]() . По
определению ортогональной суммы вектор
. По
определению ортогональной суммы вектор ![]() Т.к. L
порождают линейно независимые векторы
Т.к. L
порождают линейно независимые векторы ![]() , то
, то ![]() . Линейная независимость векторов
. Линейная независимость векторов ![]() очевидна.
Из всего выше сказанного следует, что
очевидна.
Из всего выше сказанного следует, что ![]() . Т.к.
. Т.к. ![]() , то по определению ортогональных множеств это означает,
что
, то по определению ортогональных множеств это означает,
что ![]() Подставим
значение h:
Подставим
значение h:
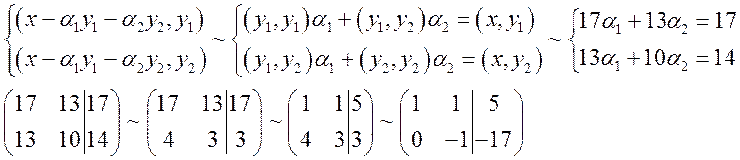
Найдем
коэффициенты ![]() :
:
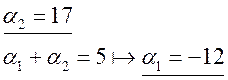
С
помощью выше описанных формул найдем ![]() :
:
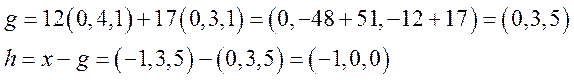
Теперь
вычислим длины векторов ![]() :
:
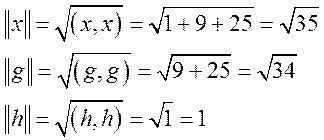
Проверим
ортогональность векторов ![]() :
:
![]()
По
формуле 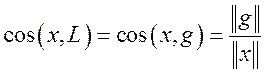 найдем угол между наклонной x
и подпространством L:
найдем угол между наклонной x
и подпространством L:
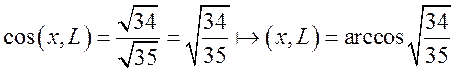 .
.
Выберем из заданной системы векторов базис:
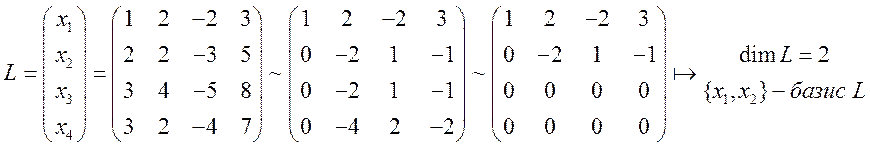
Так
как векторы базиса неортогональны, ортагонализуем их с помощью процедуры
Грама-Шмидта. Полагаем, что ![]() ,
причем
,
причем 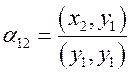 . Найдем
. Найдем ![]() :
:
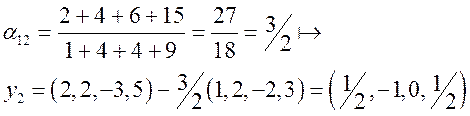
Теперь
базис подпространства L составляют ортогональные вектора ![]() . Найдем теперь вектора
. Найдем теперь вектора ![]() , так чтобы все вышеперечисленные вектора были попарно
ортогональны, т.о. мы обеспечим их линейную независимость. Вектор
, так чтобы все вышеперечисленные вектора были попарно
ортогональны, т.о. мы обеспечим их линейную независимость. Вектор ![]() мы найдем из условий:
мы найдем из условий:
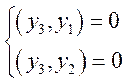
Пусть
вектор ![]() . Составим СЛАУ:
. Составим СЛАУ:
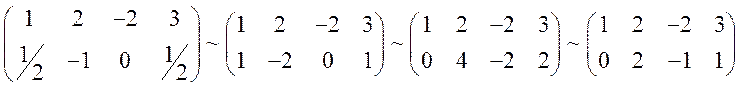
Т.к.
![]() - свободные члены, то выберем для них значения равные
2 (
- свободные члены, то выберем для них значения равные
2 (![]() ). Найдем оставшиеся координаты:
). Найдем оставшиеся координаты:
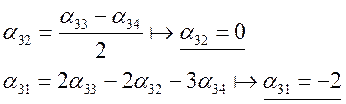
Получили,
что ![]() . Проверим полученный вектор на попарную
ортогональность:
. Проверим полученный вектор на попарную
ортогональность:
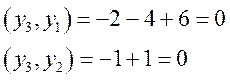
Теперь
таким же образом найдем и ![]() . Для
него должно выполняться:
. Для
него должно выполняться:
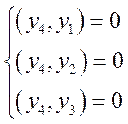
Решим СЛАУ:
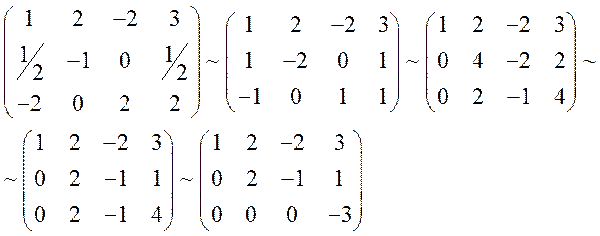
Найдем коэффициенты:
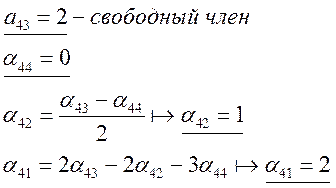
Получили
вектор ![]() . Теперь проверим его:
. Теперь проверим его:
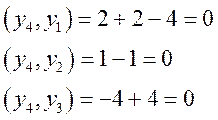
Итак
ортогональный базис пространства ![]() составляют:
составляют:
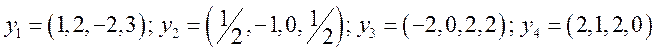
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.