Кривые второго порядка. Классификация кривых второго порядка

8.3.15. Точка А лежит на прямо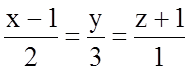й . Расстояние от точки А до плоскости  равно . Найдите координаты точки А.

     8.3.16. Составьте уравнение прямой, симметричной прямой 

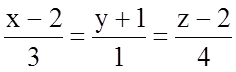 относительно плоскости .

     8.3.17. Составьте уравнения проекций на плоскость  следующих прямых:

     а) ;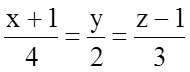

     б)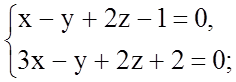

     в) .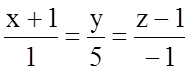

     8.3.18. Найдите угол между плоскостью  и прямой:

     а) ;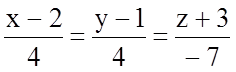

     б) .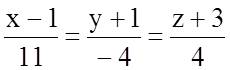

     8.3.19. Найдите точку, симметричную точке  относительно плоскости, проходящей через прямые:

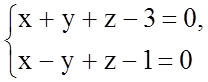        и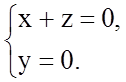        

     8.3.20. Точка А лежит на прямой

    

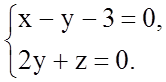
Расстояние от точки А до прямой  равно . Найдите координаты точки А.

§ 8.4. КРИВЫЕ ВТОРОГО ПОРЯДКА

     Установим на плоскости прямоугольную систему координат и рассмотрим общее уравнение второй степени

     ,                                               (8.4.1)

в котором .

     Множество всех точек плоскости, координаты которых удовлетворяют уравнению (8.4.1), называется кривой (линией) второго порядка.

     Для всякой кривой второго порядка существует прямоугольная система координат, называемая канонической, в которой уравнение этой кривой имеет один из следующих видов:

1) 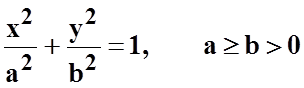          (эллипс);

2) 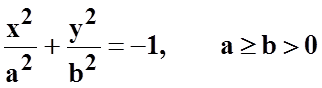          (мнимый эллипс);

3) 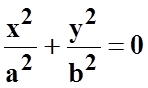          (пара мнимых пересекающихся прямых);

4) 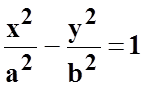          (гипербола);

5) 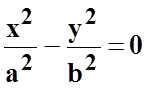          (пара пересекающихся прямых);

6)           (парабола);

7)           (пара параллельных прямых);

8)           (пара мнимых параллельных прямых);

9)           (пара совпадающих прямых).

     Уравнения 1) – 9) называются каноническими уравнениями кривых второго порядка.

     Решение задачи приведения уравнения кривой второго порядка к каноническому виду включает нахождение канонического уравнения кривой и канонической системы координат. Приведение к каноническому виду позволяет вычислить параметры кривой и определить ее расположение относительно исходной системы координат. Переход от исходной прямоугольной системы координат  к канонической  осуществляется путем поворота осей исходной системы координат вокруг точки О на некоторый угол j и последующего параллельного переноса системы координат.

     Инвариантами кривой второго порядка (8.4.1) называются такие функции от коэффициентов ее уравнения, значения которых не меняются при переходе от одной прямоугольной системы координат к другой такой же системе.

     Для кривой второго порядка (8.4.1) сумма коэффициентов при квадратах координат

     ,

определитель, составленный из коэффициентов при старших членах

     

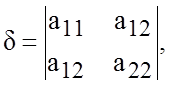
и определитель третьего порядка

    

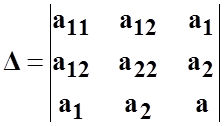
являются инвариантами.

     Значение инвариантов s, d, D можно использовать для определения типа и составления канонического уравнения кривой второго порядка.

Таблица 8.1.

Классификация кривых второго порядка, основанная на инвариантах

d>0 Кривая эллиптического типа	D¹0	sD<0.  Эллипс
		sD>0.  Мнимый эллипс
	D=0	Пара мнимых прямых, пересекающихся в действительной точке
d<0 Кривая гиперболического типа	D¹0	Гипербола
	D=0	Пара пересекающихся прямых
d=0 Кривая параболического типа	D¹0	Парабола
	D=0	Пара параллельных прямых (различных, мнимых или совпадающих)

     Рассмотрим подробнее эллипс, гиперболу и параболу.

     Эллипсом (рис. 8.1) называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек  этой плоскости, называемых фокусами эллипса, есть величина постоянная (большая, чем расстояние между фокусами). При этом не исключается совпадение фокусов эллипса. Если фокусы совпадают, то эллипс представляет собой окружность.

     Полусумму расстояний от точки эллипса до его фокусов обозначают через а, половину расстояний между фокусами – с. Если прямоугольная система координат на плоскости выбрана так, что фокусы эллипса располагаются на оси Оx симметрично относительно начала координат, то в этой системе координат эллипс задается уравнением

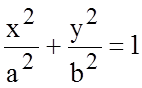     ,                                                                                                     (8.4.2)

называемым каноническим уравнением эллипса, где  .

 

Рис. 8.1

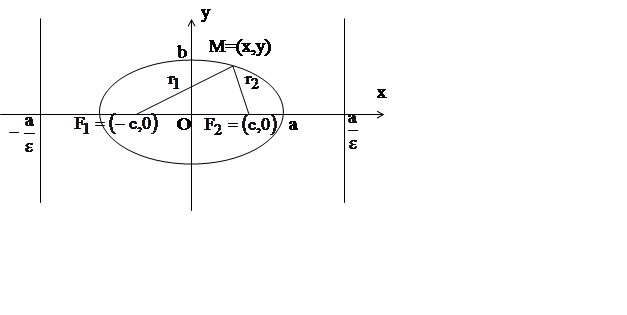      При указанном выборе прямоугольной системы координат эллипс симметричен относительно осей координат и начала координат. Оси симметрии эллипса называют его осями, а центрего симметрии – центром эллипса. Вместе с тем часто осями эллипса называют числа 2a и 2b, а числа a и b – большой и малой полуосью соответственно.

      Точки пересечения эллипса с его осями называются вершинами эллипса. Вершины эллипса имеет координаты (а,0), (–а,0), (0,b), (0,–b).

      Эксцентриситетом эллипса называется число

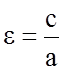      .                                                                                                               (8.4.3)

Поскольку 0£c<a, эксцентриситет эллипса 0£e<1, причем у окружности e = 0. Перепишем равенство (8.4.3) в виде

      .

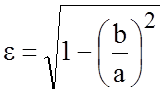Отсюда видно, что эксцентриситет характеризует форму эллипса: чем ближе e к нулю, тем больше эллипс похож на окружность; при увеличении e эллипс становится более вытянутым.