Кривые второго порядка. Классификация кривых второго порядка, страница 4

      В силу того, что результирующее преобразование прямоугольных координат определяется формулами

      ,

      ,

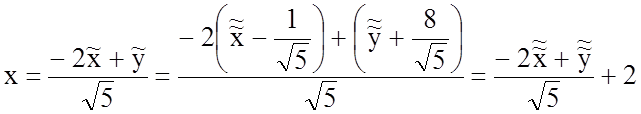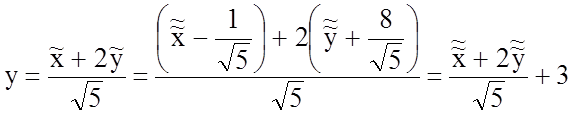каноническая система координат  имеет начало  и направляющие векторы .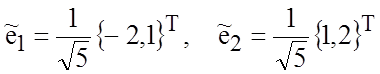

      Пример 3. Применяя теорию инвариантов, определите тип и составьте каноническое уравнение кривой

      .

      Решение. Поскольку

     

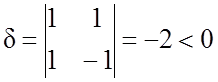
и

      ,

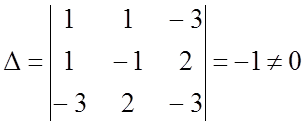в соответствии с табл. 8.1 заключаем, что это – гипербола.

      Так как s = 0, характеристический многочлен матрицы квадратичной формы  

      .

Его корни  и  позволяют записать каноническое уравнение кривой

      ,

где С находится из условия

     

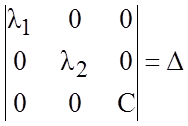
или

      .

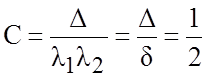      Искомое каноническое уравнение кривой

      .

      В задачах этого параграфа координаты x, y предполагаются прямоугольными.

      8.4.1. Для эллипсов  и  найдите:

      а) полуоси;

      б) фокусы;

в) эксцентриситет;

г) уравнения директрис.   

      8.4.2. Составьте уравнения эллипса, зная его фокус , соответствующую директрису x = 8 и эксцентриситет 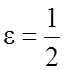. Найдите второй фокус и вторую директрису эллипса.

      8.4.3. Составьте уравнение эллипса, фокусы которого имеют координаты (1,0) и (0,1), а большая ось равна двум.

      8.4.4. Дана гипербола 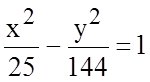. Найдите:

а) полуоси a и b;

б) фокусы;

в) эксцентриситет;

г) уравнения асимптот;

д) уравнения директрис.  

      8.4.5. Дана гипербола 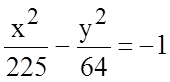. Найдите:

а) полуоси а и b;

б) фокусы;

в) эксцентриситет;

г) уравнения асимптот;

д) уравнения директрис.  

      8.4.6. Точка  принадлежит гиперболе, фокус которой , а соответствующая директриса задана уравнением . Составьте уравнение этой гиперболы.

      8.4.7. Составьте уравнение параболы, если даны ее фокус  и директриса .

      8.4.8. Даны вершина параболы  и уравнение директрисы . Составьте уравнение этой параболы.

      8.4.9. Составьте уравнение параболы, фокус которой находится в точке 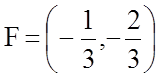 и директриса задана уравнением .

      8.4.10. Составьте уравнение кривой второго порядка, зная ее эксцентриситет , фокус  и соответствующую директрису .

      8.4.11. Определите тип кривой второго порядка, составьте ее каноническое уравнение и найдите каноническую систему координат:

      а) ;

      б) ;

      в) ;

      г) ;

      д) ;

      е) ;

      ж) ;

      з) ;

      и) ;

      к) ;

      л) .

8.4.12. Докажите, что кривая второго порядка, заданная уравнением ,

является эллипсом. Найдите длины полуосей и эксцентриситет этого эллипса, координаты центра и фокусов, составьте уравнения осей и директрис.

      8.4.13. Докажите, что кривая второго порядка, заданная уравнением ,

является гиперболой. Найдите длины полуосей и эксцентриситет этой гиперболы, координаты центра и фокусов, составьте уравнения осей, директрис и   асимптот.

      8.4.14. Докажите, что кривая второго порядка, заданная уравнением ,

является параболой. Найдите параметр этой параболы, координаты вершин и фокуса, составьте уравнения оси и директрисы.

      8.4.15. Каждое из следующих уравнений приведите к каноническому виду. Изобразите на чертеже соответствующую кривую второго порядка относительно исходной прямоугольной системы координат:

      а) ;

      б) ;

      в) ;

      г) ;

      д) ;

      е) ;

      ж) ;

      з) ;

      и) .

      8.4.16. Применяя теорию инвариантов, определите тип и составьте каноническое уравнение кривой:

      а) ;

      б) ;

      в) ;

      г) ;

      д) ;

      е) .