Кривые второго порядка. Классификация кривых второго порядка, страница 2

      Пусть  – произвольная точка эллипса,  и  – расстояния от точки М до фокусов F₁ и F₂ соответственно. Числа r₁ и r₂ называются фокальными радиусами точки М эллипса и вычисляются по формулам

      .

      Директрисами отличного от окружности эллипса с каноническим уравнением (8.4.2) называются две прямые

      .

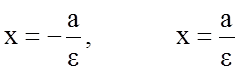      Директрисы эллипса расположены вне эллипса (рис.8.1).

      Отношение фокального радиуса  точки M эллипса к расстоянию  от этой точки до отвечающей фокусу  директрисы равно эксцентриситету e этого эллипса (фокус и директриса считаются соответствующими, если они расположены по одну сторону от центра эллипса).

      Гиперболой (рис. 8.2) называется геометрическое место точек плоскости, для которых модуль разности расстояний до двух фиксированных точек  и  этой плоскости, называемых фокусами гиперболы, есть величина постоянная (не равная нулю и меньшая, чем расстояние между фокусами).

      Пусть расстояние между фокусами равно 2с, а указанный модуль разности расстояний равен 2а. Выберем прямоугольную систему координат так же, как и для эллипса. В этой системе координат гипербола задается уравнением

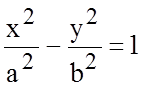      ,                                                                                                    (8.4.4)

называемым каноническим уравнением гиперболы, где .

 

Рис. 8.2

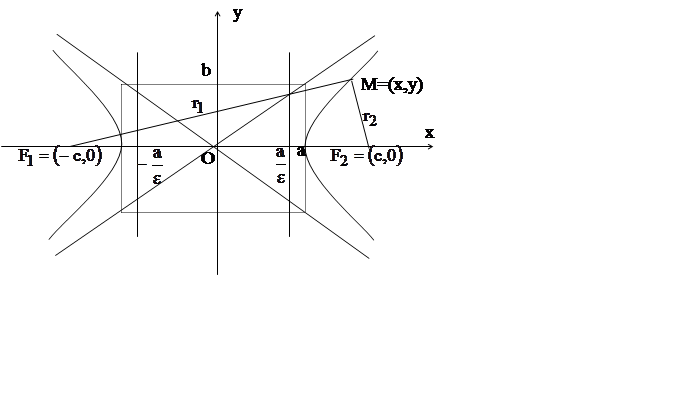
      При данном выборе прямоугольной системы координат оси координат являются осями симметрии гиперболы, а начало координат – ее центром симметрии. Оси симметрии гиперболы называют ее осями, а центр симметрии– центром гиперболы. Прямоугольник со сторонами 2a и 2b, расположенный, как показано на рис. 8.2, называется основным прямоугольником гиперболы. Числа 2a и 2b – оси гиперболы, а числа a и b – ее полуоси. Прямые, являющиеся продолжением диагоналей основного прямоугольника, образуют асимптоты гиперболы

      .

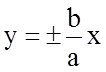      Точки пересечения гиперболы с осью Ox называются вершинами гиперболы. Вершины гиперболы имеют координаты (а,0), (–а,0).

      Эксцентриситетом гиперболы называется число

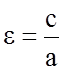      .                                                                                                               (8.4.5)

Поскольку с > a, эксцентриситет гиперболы e > 1. Перепишем равенство (8.4.5) в виде

      .

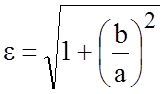Отсюда видно, что эксцентриситет характеризует форму основного прямоугольника и, следовательно, форму самой гиперболы: чем меньше e, больше вытягивается основной прямоугольник, а вслед за ним и сама гипербола вдоль оси Ox.

      Пусть  – произвольная точка гиперболы,  и  – расстояния от точки М до фокусов F₁ и F₂ соответственно. Числа r₁ и r₂ называются фокальными радиусами точки М гиперболы и вычисляются по формулам

     

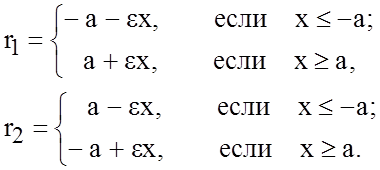
      Директрисами гиперболы с каноническим уравнением (8.4.4) называются две прямые

      .

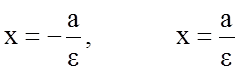      Директрисы гиперболы пересекают основной прямоугольник и проходят между центром и соответствующей вершиной гиперболы (рис.8.2).

      Отношение фокального радиуса  точки M гиперболы к расстоянию  от этой точки до отвечающей фокусу  директрисы равно эксцентриситету e этой гиперболы (фокус и директриса считаются соответствующими, если они расположены по одну сторону от центра гиперболы).

      Параболой (рис. 8.3) называется геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки F (фокуса параболы) этой плоскости равно расстоянию до некоторой фиксированной прямой (директрисы параболы), также расположенной в рассматриваемой плоскости.