Линейные операторы и матрицы
Пусть дан линейный оператор А, действующий из n-мерного
пространства Х в m-мерное пространство Y. Выберем
некоторый базис е![]() , е
, е![]() ,…,е
,…,е![]() в Х.
в Х.
Тогда
![]() x
x![]() X
X
x =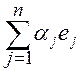 , A·x =
, A·x =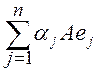 .
.
Другими
словами, линейный оператор A:X![]() Y
полностью определяется совокупностью образов Ae
Y
полностью определяется совокупностью образов Ae![]() , Ae
, Ae![]() ,…, Ae
,…, Ae![]() базисных векторов е
базисных векторов е![]() , е
, е![]() ,…,е
,…,е![]() и
и
y = Ax, y![]() L(Ae
L(Ae![]() , Ae
, Ae![]() ,…, Ae
,…, Ae![]() ).
).
Зафиксируем
в пространстве Y базис g![]() , g
, g![]() ,…,g
,…,g![]() . Тогда
. Тогда
![]() =a
=a![]() g
g![]() +…+a
+…+a![]() g
g![]() , j =1, 2,…, n
, j =1, 2,…, n
Коэффициенты
a![]() определяют матрицу A
определяют матрицу A![]() из m строк и n столбцов, которая называется матрицей
оператора A в базисах е
из m строк и n столбцов, которая называется матрицей
оператора A в базисах е![]() , е
, е![]() ,…,е
,…,е![]() и g
и g![]() , g
, g![]() ,…,g
,…,g![]() :
:
A![]() =
=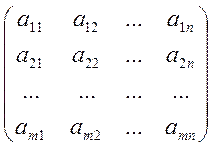 .
.
Столбцами матрицы оператора служат координаты векторов Ae![]() , Ae
, Ae![]() ,…, Ae
,…, Ae![]() в базисе g
в базисе g![]() , g
, g![]() ,…,g
,…,g![]() . Для того, чтобы определить элемент a
. Для того, чтобы определить элемент a![]() матрицы оператора A, нужно найти образ Ae
матрицы оператора A, нужно найти образ Ae![]() и взять его координату в базисе
и взять его координату в базисе
g![]() , g
, g![]() ,…,g
,…,g![]() , т.е.
, т.е.
a![]() =
=![]() .
.
Рассмотрим произвольный вектор x![]() X и его образ y=Ax:
X и его образ y=Ax:
x=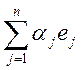 , y =
, y =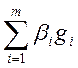 . (1)
. (1)
Тогда
y=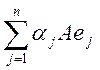 =
=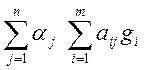 =
= 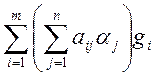 .
.
Сравнивая правую часть этого равенства с разложением (1) для вектора y, имеем
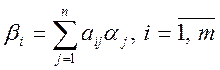
Обозначив
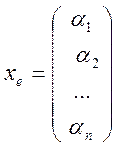 ,
, 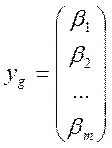 ,
получим
,
получим
![]() (2)
(2)
Таким образом, всякий линейный оператор при фиксированных базисах в пространствах X и Y порождает соотношение (2), связывающее координаты образа и прообраза.
Для того чтобы по координатам прообраза определить координаты образа, достаточно вычислить левую часть этого соотношения.
Для определения координат прообраза по известным координатам вектора ![]() приходится решать СЛАУ (2) относительно
вектора
приходится решать СЛАУ (2) относительно
вектора ![]() . Матрица этой СЛАУ совпадает с матрицей
оператора.
. Матрица этой СЛАУ совпадает с матрицей
оператора.
Докажем, что при фиксированных базисах пространств между линейными операторами и прямоугольными матрицами существует взаимнооднозначное соответствие.
Мы
уже показали, что каждый оператор А при фиксированных базисах определяет
некоторую матрицу А![]() . Возьмём
теперь произвольную матрицу А
. Возьмём
теперь произвольную матрицу А![]() размером
m
размером
m![]() n. При
фиксированных базисах в пространствах X и Y соотношение
(2) ставит в соответствие каждому вектору x
n. При
фиксированных базисах в пространствах X и Y соотношение
(2) ставит в соответствие каждому вектору x![]() X некоторый вектор y
X некоторый вектор y![]() Y. Ясно, что это соответствие –
линейный оператор:
Y. Ясно, что это соответствие –
линейный оператор:
![]() .
.
Построим
матрицу оператора А в базисах е![]() ,е
,е![]() ,…,е
,…,е![]() , g
, g![]() ,g
,g![]() ,…,g
,…,g![]() :
:
![]()
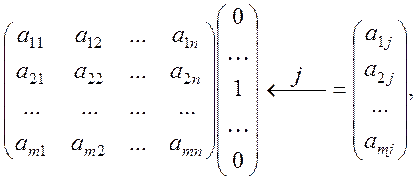
![]() ,
,
т.е.
построенная матрица совпадает с А![]() .
.
Операции над матрицами и операторами
Поскольку всякий линейный оператор при фиксированных базисах пространств однозначно определяется своей матрицей, введенные ранее операции над операторами соответствуют вполне определенным операциям над матрицами.
Условимся обозначать операторы и их матрицы одними и теми же буквами, без каких-либо индексов, относящихся к базисам.
Пусть A:X![]() Y, B:X
Y, B:X![]() Y и е
Y и е![]() , е
, е![]() ,…,е
,…,е![]() - базис X, g
- базис X, g![]() , g
, g![]() ,…,g
,…,g![]() - базис Y.
- базис Y.
Равные операторы имеют одну и ту же матрицу.
Доказательство:
Действительно,
a![]() =
=![]() =
=![]() =
b
=
b![]() , i =
, i =![]() , j =
, j =![]() .
.
Рассмотрим оператор С =А+В:
![]() .
.
При сложении операторов матрицы операторов складываются.
Аналогичное преобразование матриц операторов происходит при умножении линейного оператора на число:
![]() .
.
Таким образом, пространство линейных операторов
w![]() изоморфно пространству
прямоугольных матриц размером m
изоморфно пространству
прямоугольных матриц размером m![]() n
с элементами из F.
n
с элементами из F.
Следовательно, размерности этих пространств равны. Множество
матриц порядка m![]() n представляет
собой линейное пространство размерности m·n.
Одним из базисов этого пространства может служить система матриц:
n представляет
собой линейное пространство размерности m·n.
Одним из базисов этого пространства может служить система матриц:
![]() , где элементы
, где элементы ![]() матрицы
матрицы
![]() определяются равенствами:
определяются равенствами:
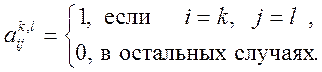
Возьмем m=2, n=3. Тогда:
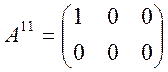 ,
, 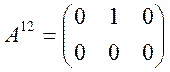 ,
, 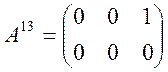 ,
,
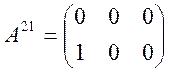 ,
, 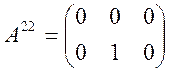 ,
, 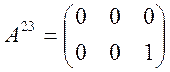 .
.
Отсюда следует, что линейное пространство операторов, действующих из X в Y, есть конечномерное пространство размерности m·n.
Если оператор A:X![]() Y, B:Y
Y, B:Y![]() Z, C:X
Z, C:X![]() Z, то
произведению операторов С=ВА соответствует произведение матриц. Действительно,
пусть е
Z, то
произведению операторов С=ВА соответствует произведение матриц. Действительно,
пусть е![]() , е
, е![]() ,…,е
,…,е![]() - базис в X, f
- базис в X, f![]() , f
, f![]() ,…,f
,…,f![]() - базис в Y, g
- базис в Y, g![]() , g
, g![]() ,…,g
,…,g![]() - базис в Z. Тогда:
- базис в Z. Тогда:
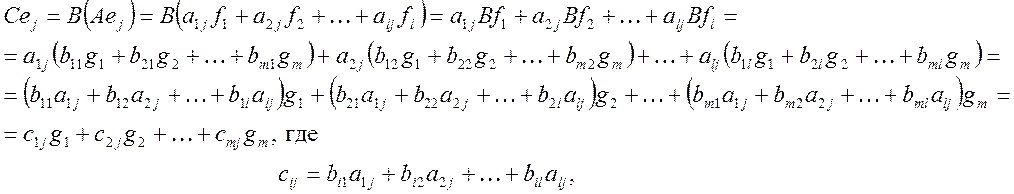 Пусть A:X
Пусть A:X![]() Y, е
Y, е![]() , е
, е![]() ,…,е
,…,е![]() - базис X, g
- базис X, g![]() , g
, g![]() ,…,g
,…,g![]() - базис Y. По определению, рангом оператора А
называется размерность образа
- базис Y. По определению, рангом оператора А
называется размерность образа ![]() |
|![]() . Но
. Но ![]() и
совпадает с максимальным числом линейно-независимых векторов среди Ae
и
совпадает с максимальным числом линейно-независимых векторов среди Ae![]() , Ae
, Ae![]() ,…, Ae
,…, Ae![]() . Учитывая, что столбцы матрицы А есть координаты
. Учитывая, что столбцы матрицы А есть координаты ![]() в базисе g
в базисе g![]() , g
, g![]() ,…,g
,…,g![]() , задача сводится к нахождению максимального числа
линейно-независимых столбцов матрицы А. Другими словами, ранг оператора А
равен рангу матрицы оператора А.
, задача сводится к нахождению максимального числа
линейно-независимых столбцов матрицы А. Другими словами, ранг оператора А
равен рангу матрицы оператора А.
Дефект оператора- размерность ядра ![]() |
|![]() , т.е.
, т.е. ![]() .
.
Пусть x![]() . Тогда
для координат x в базисе е
. Тогда
для координат x в базисе е![]() , е
, е![]() ,…,е
,…,е![]() выполняется
условие Ax
выполняется
условие Ax![]() 0.
Верно и обратное. Таким образом, дефект
равен размерности пространства решений однородной СЛАУ и равен
0.
Верно и обратное. Таким образом, дефект
равен размерности пространства решений однородной СЛАУ и равен ![]() .
.
Пусть A:X![]() X и А
– невырожденный оператор. Тогда dimX=rgA=n и соответствующая n×n-матрица
будет иметь n–линейно-независимых столбцов, т.е. ее определитель не
равен нулю. Верно и обратное. Таким образом, линейный оператор невырожден
тогда и только тогда, когда определитель его матрицы не равен нулю.
X и А
– невырожденный оператор. Тогда dimX=rgA=n и соответствующая n×n-матрица
будет иметь n–линейно-независимых столбцов, т.е. ее определитель не
равен нулю. Верно и обратное. Таким образом, линейный оператор невырожден
тогда и только тогда, когда определитель его матрицы не равен нулю.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.