б) ![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() .
.
§ 8.5. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Геометрическое
место точек 3 – мерного пространства, координаты которых в некоторой
прямоугольной системе координат ![]() удовлетворяют уравнению
удовлетворяют уравнению
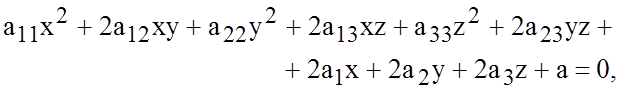 (8.5.1)
(8.5.1)
где
хотя бы один из коэффициентов ![]() не равен нулю, называется поверхностью второго порядка.
не равен нулю, называется поверхностью второго порядка.
Для
любой поверхности второго порядка существует прямоугольная система координат ![]() , в
которой уравнение этой поверхности имеет один из следующих 17 видов:
, в
которой уравнение этой поверхности имеет один из следующих 17 видов:
1)
эллипсоид 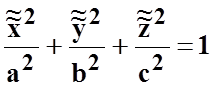 (рис. 8.4);
(рис. 8.4);
2)
мнимый эллипсоид 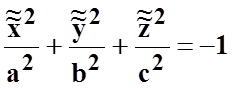 ;
;
3)
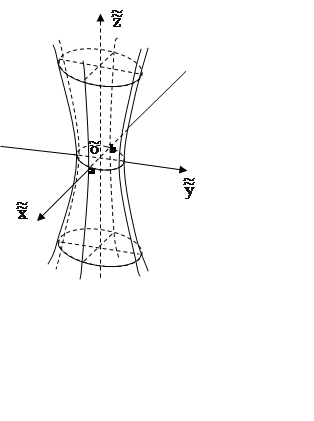
однополостный гиперболоид 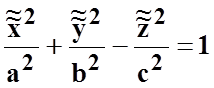 (рис.
8.5);
(рис.
8.5);
4)
двуполостный гиперболоид 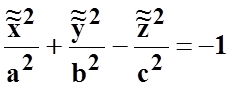 (рис.
8.6);
(рис.
8.6);
5)
конус 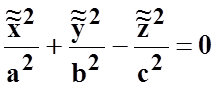 (рис. 8.7);
(рис. 8.7);
6)
мнимый конус 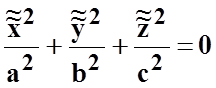 ;
;
7)
эллиптический параболоид 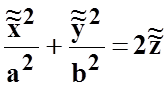 (рис.
8.8);
(рис.
8.8);
8)
гиперболический параболоид 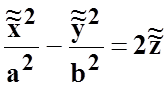 (рис.
8.9);
(рис.
8.9);
9)
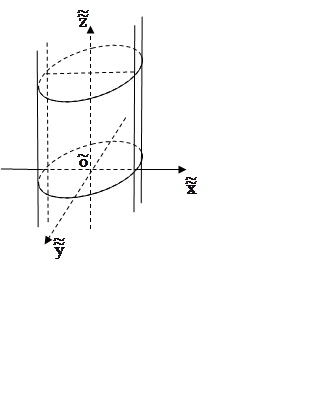
эллиптический цилиндр 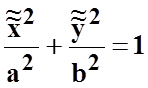 (рис.
8.10);
(рис.
8.10);
10)
мнимый эллиптический цилиндр 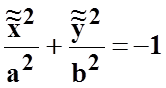 ;
;
11)
гиперболический цилиндр 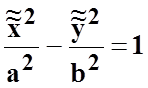 (рис.
8.11);
(рис.
8.11);
12)
параболический цилиндр ![]() (рис.
8.12);
(рис.
8.12);
13)
пара пересекающихся плоскостей 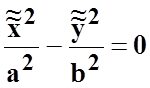 ;
;
14)
пара мнимых пересекающихся плоскостей 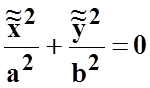 ;
;
15)
пара параллельных плоскостей ![]() ;
;
16)
пара мнимых параллельных плоскостей ![]() ;
;
17)
пара совпадающих плоскостей ![]() .
.
Уравнения 1) – 17) называются каноническими уравнениями поверхностей второго порядка.
 |
|||
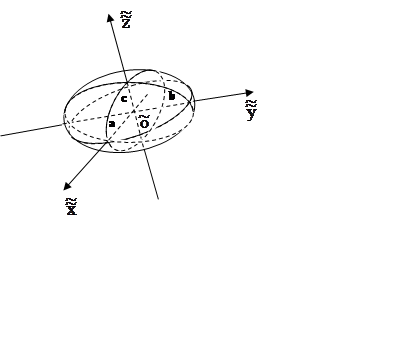 |
|||
Рис. 8.4 Рис. 8.5
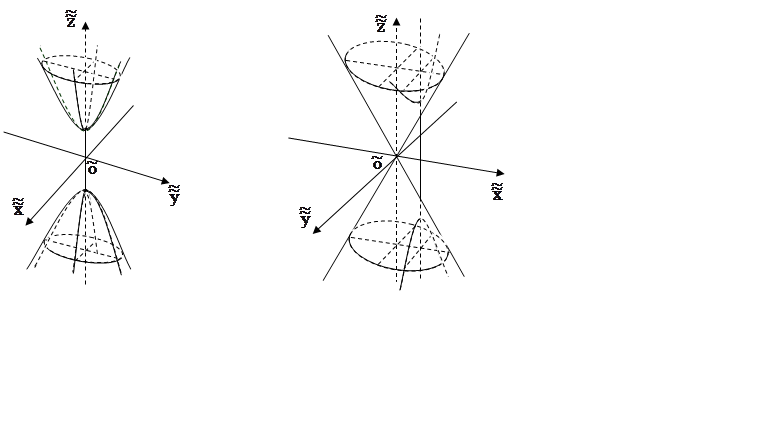 |
Рис. 8.6 Рис. 8.7
 |
|||
 |
|||
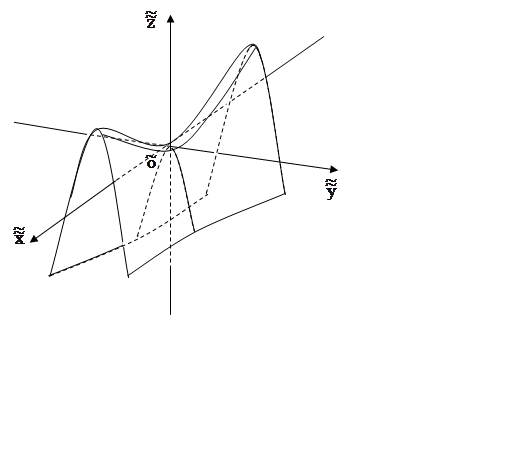 |
Рис. 8.8 Рис. 8.10
Рис. 8.9
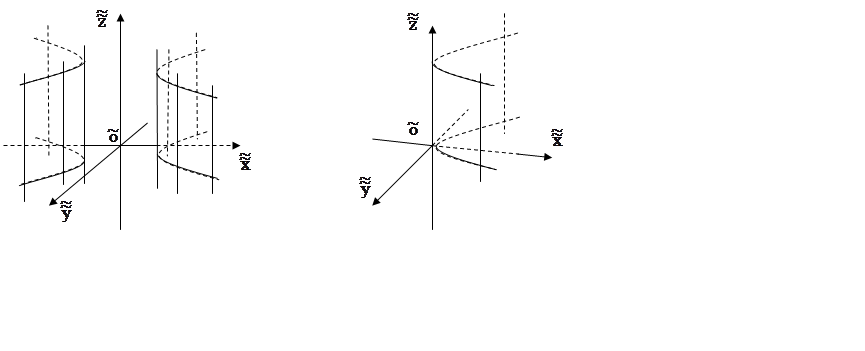 |
Рис. 8.11 Рис. 8.12
![]() ,
,
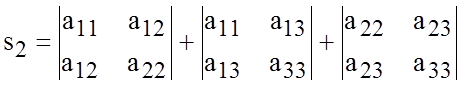 ,
,
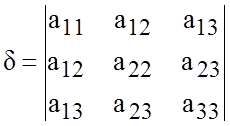 ,
,
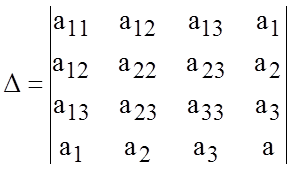 .
.
Их значения не меняются при повороте и параллельном переносе осей координат.
Пример 1. Поверхность задана уравнением в прямоугольной системе координат
![]() .
.
Найдите каноническую систему координат и каноническое уравнение этой поверхности. Определите тип поверхности.
Решение.
Найдем сначала ортогональное преобразование переменных, приводящее матрицу А
квадратичной формы ![]() к диагональному виду.
к диагональному виду.
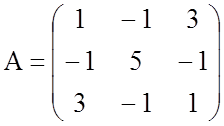 .
.
Ее характеристический многочлен
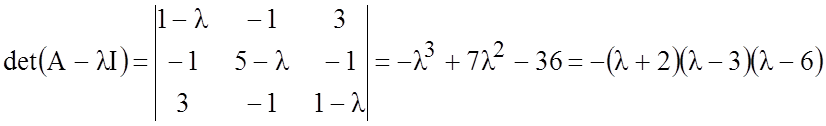 .
.
Следовательно,
матрица А имеет собственные значения ![]()
![]() .
.
Для
нахождения собственных векторов матрицы А решаем однородные системы линейных
уравнений с матрицами ![]() соответственно и выделяем по одному ненулевому решению:
соответственно и выделяем по одному ненулевому решению:
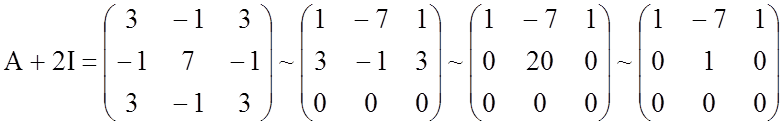 ,
,
![]() ;
;
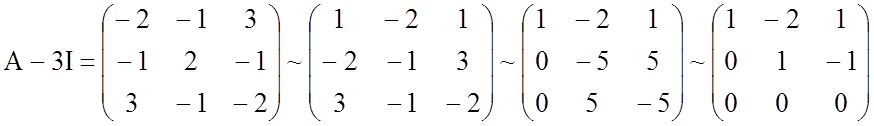 ,
,
![]() ;
;
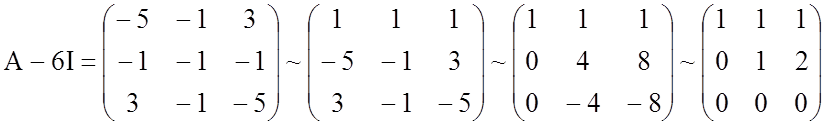 ,
,
![]() .
.
Векторы
![]() ортогональны
друг другу как собственные векторы симметричной матрицы, соответствующие
различным собственным значениям. Нормируя их, получаем
ортогональны
друг другу как собственные векторы симметричной матрицы, соответствующие
различным собственным значениям. Нормируя их, получаем
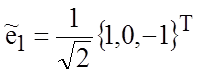 ,
,
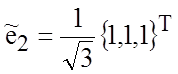 ,
,
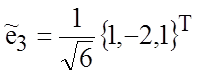
и матрицу перехода Р к новому ортонормированному базису
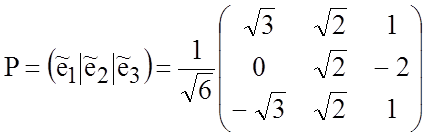 .
.
Проверим правильность нахождения матрицы Р:
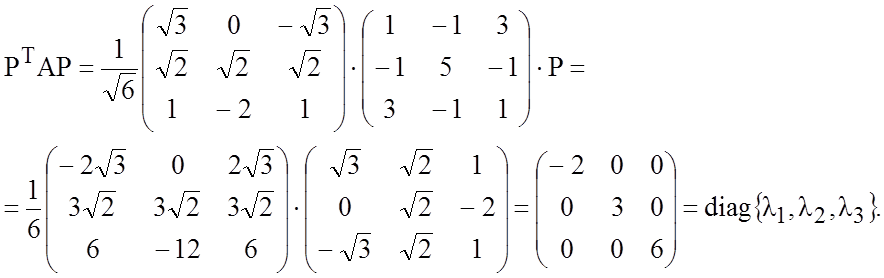
Матрица Р найдена верно.
Применяя к исходному уравнению ортогональное преобразование координат
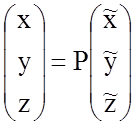 ,
,
получаем
новое уравнение поверхности в прямоугольной системе координат со старым центром
О и направляющими векторами ![]() :
:
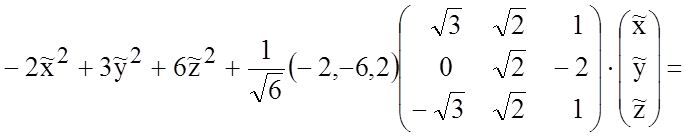
![]()
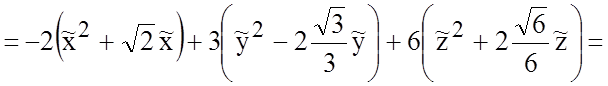
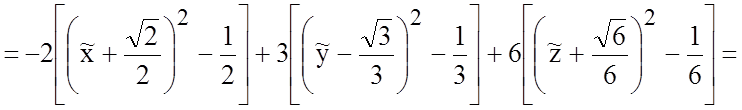
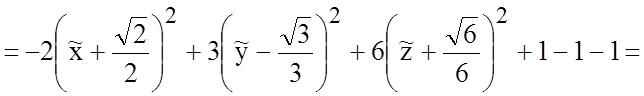
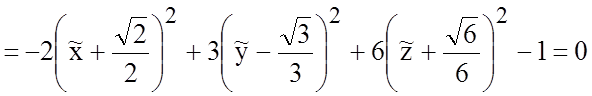 .
.
Выполняя
параллельный перенос системы координат ![]() по формулам
по формулам
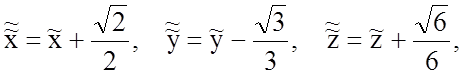
приходим к уравнению
![]()
или
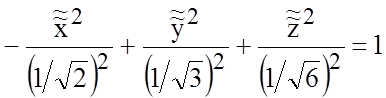 .
.
Это
– каноническое уравнение двуполостного гиперболоида в прямоугольной системе
координат ![]() .
.
Вычислим
координаты начала ![]() канонической системы координат в старой прямоугольной системе
координат. Поскольку
канонической системы координат в старой прямоугольной системе
координат. Поскольку
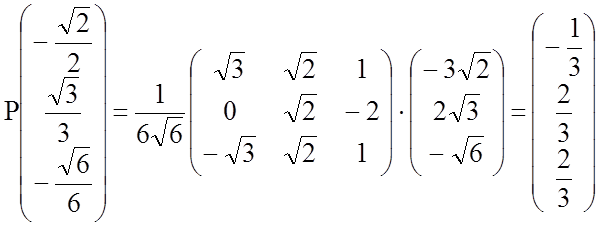 ,
,
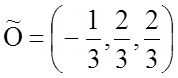 .
.
Пример 2. Исследуйте поверхность второго порядка, заданную в прямоугольной системе координат уравнением
![]() .
.
Решение.
Начнем с приведения квадратичной формы ![]() к каноническому виду. Матрицей этой квадратичной
формы является матрица
к каноническому виду. Матрицей этой квадратичной
формы является матрица
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.