Системы линейных алгебраических уравнений

Системы линейных алгебраических уравнений

Системы линейных уравнений и линейная зависимость

Пусть даны векторы  из n-мерного линейного пространства  над полем . Требуется установить, является ли вектор  линейной комбинацией . Запишем

и попытаемся найти коэффициенты . Выберем базис в . В этом базисе векторы  задаются своими координатами:

     ….,      

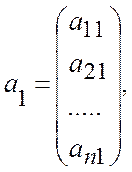
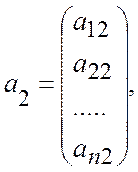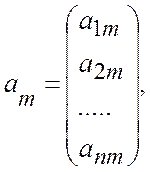
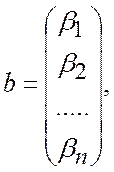
так что предыдущее соотношение принимает вид

=.

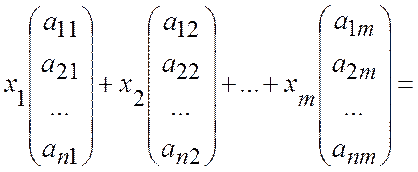
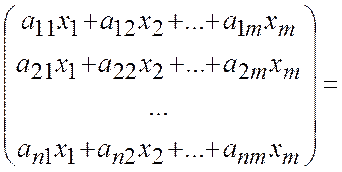
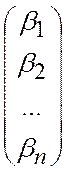В результате приходим к системе линейных алгебраических уравнений

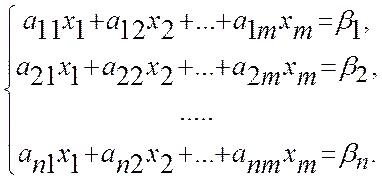
или, в матричном виде, .

Ранг матрицы

Будем рассматривать различные миноры -го порядка (т.е. определители подматриц, образованных из элементов, стоящих на пересечении строк и  столбцов) матрицы. .

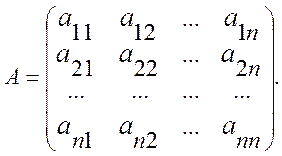
Предположим, что хотя бы один из элементов  матрицы  отличен от нуля.

Опр. Рангом матрицы  (пишут ) называется такое натуральное число ,что

1.  Матрица  имеет минор -го порядка, не равный нулю;

2.  Всякий минор  порядка матрицы  равен нулю.

Если  , то . В противном случае .

Отличный от нуля минор -го порядка называется базисным минором (естественно, у матрицы  может быть несколько миноров -го порядка, отличных от нуля) матрицы . Столбцы (строки), на которых построен базисный минор, называют базисными столбцами (строками).

Теорема 1. Любой столбец матрицы  являются линейной комбинацией ее базисных столбцов (базисных строк).

Доказательство. Поскольку при произвольных переменах столбцов (или строк) определитель сохраняет свойство равенства нулю, можно, не ограничивая общности, считать, что базисный минор расположен на первых  строках и первых  столбцах матрицы  (). Рассмотрим определитель -го порядка

,

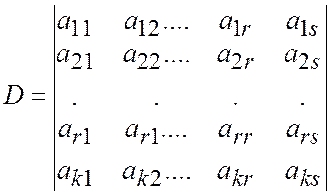где -любое число от 1 до m, а -любое число от 1 до n.

Если , то , т.к. две строки определителя одинаковы.

Если , то , т.к. два столбца определителя одинаковы.

Если  и , то  как минор -го порядка матрицы .

Таким образом .

Разложим определитель по последней строке:

,    (1)

где  - алгебраические дополнения элементов  соответственно. Эти алгебраические дополнения не зависят от номера . Обозначив их

,  , … ,, , из (1) при

получим:

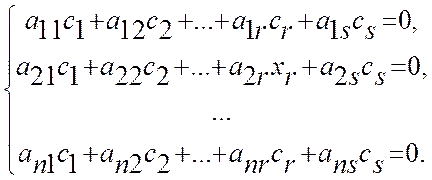
Учитывая, что , т.к. алгебраическое дополнение  образуется базисным минором, мы можем поделить каждое из полученных последних равенств на  и, обозначив

,

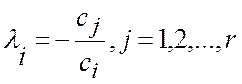получим

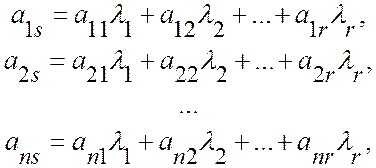
т.е. -й столбец  является линейной комбинацией первых  столбцов (базисных столбцов).

Теорема 2. Если один из столбцов определителя  является линейной комбинацией других его столбцов, то .

Доказательство. Пусть -й столбец матрицы  есть линейная комбинация -го столбцов с коэффициентами . Тогда, вычитая из -го столбца -й столбцы, умноженные на  соответственно, мы не изменим , но при этом -й столбец станет нулевым.

Теорема 3. Если определитель , то у него имеется столбец, являющийся линейной комбинацией других столбцов.

Доказательство. Т.к. , то базисный минор имеет порядок , где  - порядок . Столбец, не вошедший в число базисных, по теореме 1 будет линейной комбинацией базисных столбцов.

Теорема 4.Определитель  тогда и только тогда, когда между его столбцами существует линейная зависимость.

Доказательство очевидно.

Следствие. Определитель  тогда и только тогда, когда его строки линейно зависимы.

Будем рассматривать матрицу  как совокупность столбцов

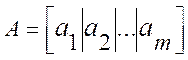
и образуем линейную оболочку .

Теорема 5. Ранг системы векторов–столбцов матрицы  равен рангу матрицы. Векторы, отвечающие базисным столбцам , образуют базу системы векторов-столбцов матрицы .

Теорема 5а. Размерность линейной оболочки системы векторов-столбцов матрицы  равна рангу матрицы. Векторы, отвечающие базисным столбцам , образуют базис линейной оболочки.

Доказательство. Пусть (для определенности) базисными являются первые  столбцов матрицы . Эти столбцы линейно независимы, т.к. в противном случае определитель -го порядка, построенный на этих столбцах и каких-либо  строках, оказался бы равен нулю, т.е. нулю был бы равен базисный минор, что противоречит определению ранга. По теореме 1 остальные столбцы (как и базисные)  .

Теорема 6. Если ранг матрицы  меньше, чем число ее столбцов, то столбцы  линейно зависимы. Если ранг  равен числу столбцов, то столбцы  линейно независимы.

Теорема 7. Всякие  cтолбцов матрицы  ранга  линейно зависимы.

Теорема 8. Ранг любой матрицы равен максимальному числу линейно независимых столбцов.

Теорема 9. Максимальное число линейно независимых строк любой матрицы совпадает с максимальным числом линейно независимых столбцов.

Однородные системы линейных алгебраических уравнений

или

,

где , .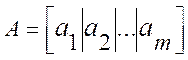

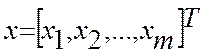Однородная система всегда совместна, т.к. она всегда обладает тривиальным (или нулевым) решением .

Возникает вопрос о том, при каких условиях однородная система имеет, кроме указанного тривиального решения, еще и другие решения (т.е. является нетривиально совместной). Это вопрос решается довольно просто. Заметим, что существование нетривиального решения системы  эквивалентно линейной зависимости столбцов матрицы , т.к. линейная зависимость столбцов матрицы  означает, что существуют числа , не все равные нулю, и такие, что

.

Теорема 10.

а). Однородная СЛАУ нетривиально совместна тогда и только тогда, когда ранг  меньше числа неизвестных.

б). Если ранг матрицы  равен числу неизвестных, то однородная система линейных уравнений не имеет ненулевых решений.

в). Если ранг  меньше числа неизвестных, то ненулевые решения существуют.

Доказательство очевидно.

Неоднородные системы линейных алгебраических уравнений.

.

 - основная матрица системы,  - расширенная матрица системы.

Теорема 11 (теорема Кронекера-Капелли). Неоднородная система линейных алгебраических уравнений совместна тогда и только тогда, когда .

Доказательство. Необходимость. Пусть система совместна. Следовательно,  есть линейная комбинация столбцов матрицы . Это эквивалентно тому, что .

Достаточность. Если , то  базисных столбцов в  будут базисными и в . По теореме 1  представляет собой некоторую линейную комбинацию базисных столбцов и представляет собой линейную комбинацию всех столбцов основной матрицы. Т.е. система совместна.

Рассмотрим однородную систему линейных алгебраических уравнений , предполагая, что , число неизвестных –  и базисный минор расположен в левом верхнем углу матрицы .