Системы линейных алгебраических уравнений, страница 3

2. Каждый элемент из  соответствует при этом одному и только одному элементу из .

Свойства изоморфизма:

1.  При изоморфизме  переводит в

.

Поскольку , то .

2.  Линейно независимая система векторов в  переводит в линейно независимую систему векторов в .

Пусть  – линейно независимая система векторов из , , .

Покажем, что система векторов {} линейно независима:

Отсюда следует, что

 

т.к.  в силу того, что

 - линейно независимы   

Доказанное позволяет утверждать, что если два конечномерных линейных пространства изоморфны, то максимальное число линейно независимых векторов в каждом из этих пространств одно и то же. Иначе, два изоморфных пространства должны иметь одинаковую размерность. Таким образом, пространства разной размерности изоморфными быть не могут.

Теорема Изоморфизма Все конечномерные пространства, заданные над одним и тем же полем, изоморфны, если и только если они имеют одинаковую размерность.

Доказательство.  Необходимость только что доказана.

Достаточность. Пусть . Покажем, что  изоморфно .

Выберем какой-нибудь базис  в пространстве  и базис  в пространстве . Каждому вектору  пространства  поставим в соответствие вектор  пространства . Установление соответствия будет взаимно однозначным, т.к. разложение по базису единственно. Покажем, что условия изоморфизма выполнены:

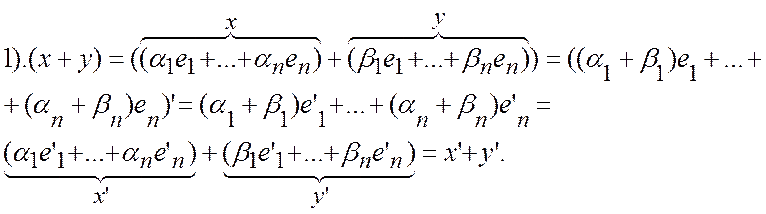
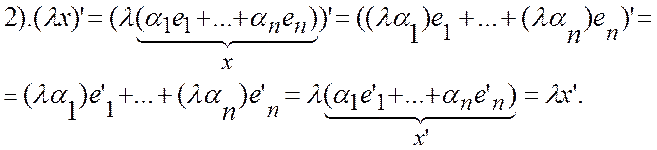
Эта теорема очень важна. Различная природа элементов линейных пространств  и , заданных над одним и тем же полем, не играет роли. Если , то  и  неразличимы. Можно было бы ввести одно какое–либо n-мерное пространство и только его изучать. Часто в качестве такого пространства выбирают .

Поскольку задано некоторое поле . Рассмотрим множество, элементами которого являются всевозможные упорядоченные наборы из n чисел  поля . Если  есть элемент этого множества, будем писать . Операции сложения и умножение на число  из поля  определим следующим образом.

;

.

Можно показать, что все аксиомы линейного пространства выполнены. В частности,   ,       .

Это пространство является n-мерным и один из его базисов легко сразу же указать. А именно,

,

,

.

Т.к. , то числа  будем называть координатами вектора . Пространство подобного типа называется арифметическим пространством. Если , то обозначают  ; если  , то -  В общем случае - .

Общее изучение линейных пространств позволяет понять их важнейшие свойства, которые не зависят от базиса.

Отношение изоморфизма является отношением эквивалентности, т.е. оно рефлексивно, симметрично и транзитивно. Поэтому совокупность всех линейных пространств над данным полем  распадается на непересекающиеся классы изоморфных пространств. Любые два линейных пространства одной и той же размерности изоморфны (разной размерности – нет). Для  существует единственный класс изоморфных пространств.

Иногда теорема  изоморфизма формулируется так:

Всякое n-мерное векторное пространство  над полем  изоморфно .

Доказательство. Пусть  - базис в  и каждый  разлагается по базису в виде линейной комбинации  единственным образом. Т.о. . Это соответствие и есть изоморфизм  и .