Системы линейных алгебраических уравнений, страница 2

Пусть  и  - два произвольных решения этой системы. Тогда

,

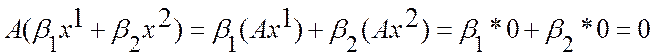т.е. совокупность всех решений однородной системы линейных алгебраических уравнений образует подпространство линейного пространства .

Поскольку всякое решение первых  уравнений нашей системы удовлетворяет всем последующим ее уравнениям, ограничимся рассмотрением уравнений

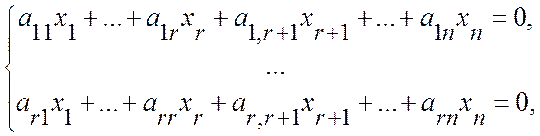
откуда получаем:

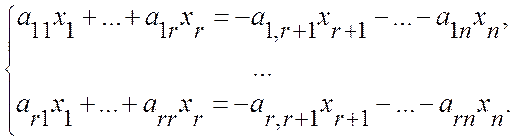
Получая последовательно

,      … 

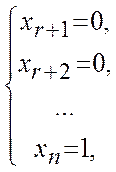
находим  линейно независимых решений:

,    ,  …,    .

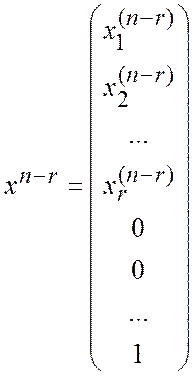Покажем, что всякое решение 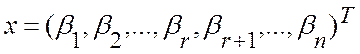 однородной системы есть линейная комбинация векторов . Рассмотрим вектор

,

также являющийся (как линейная комбинация решений) решением системы, т.е.

.

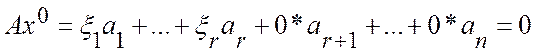Учитывая, что

,

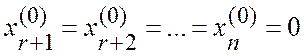отсюда вытекает равенство нулю . Следовательно,  и

.

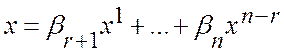Опр. Совокупность линейно независимых решений  однородной системы линейных алгебраических уравнений называется фундаментальной системой решений, если любое решение этой системы может быть представлено в виде линейной комбинации векторов этой совокупности.

Таким образом, для однородной системы, если , то система имеет единственное нулевое решение, если же , то множество решений системы образует подпространство в  размерности , и базисом этого подпространства является фундаментальная система решений.

Рассмотрим теперь неоднородную систему линейных алгебраических уравнений .

Пусть  и  - два произвольных решения этой системы. Тогда

,

т.е разность ,  является решением однородной системы , что позволяет сформулировать следующую теорему:

Теорема 12. Общее решение неоднородной системы линейных алгебраических уравнений есть сумма частного решения неоднородной системы и общего решения соответствующей однородной системы.

Преобразование координат при изменении базиса

Пусть  и  - два произвольных базиса -мерного линейного пространства . Выразим каждый вектор второго базиса чрез первый:

,

,

.

Это означает, что переход от первого базиса  ко второму базису  задается матрицей

,

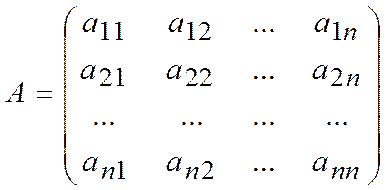определитель которой заведомо отличен от нуля, ибо в противном случае строки этой матрицы (а стало быть, и базисные элементы ) оказались бы линейно зависимыми.

Пусть далее  – произвольный вектор из . Тогда

.

Подставив в это равенство вместо  их выражения, получим

.

Отсюда, в силу линейной независимости , получим

,

,

.

или, в матричном виде

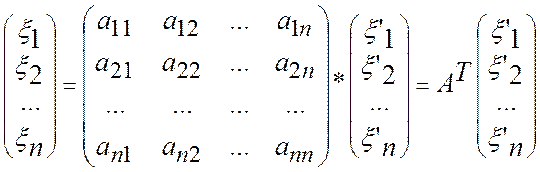
и

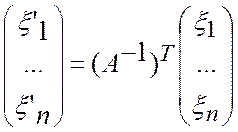
Изоморфизм линейных пространств

Пространства, устроенные одинаково по отношению к операциям сложениям векторов и умножения вектора на число, будем считать обладающими одинаковыми свойствами или изоморфными.

Опр. Два линейных пространства  и  заданные над одним и тем же полем , называются изоморфными, если между векторами  и  можно установить такое взаимно однозначное соответствие , что, если вектору  соответствует вектор , а вектору  соответствует  вектор, то

1)  вектору  соответствует ;

2)  вектору  соответствует , :

Другими словами,

, .

Заметим, что соответствие, установленное между элементами двух множеств  и , называется взаимно однозначным, если:

1. Каждому элементу из  соответствует один и только один элемент из .