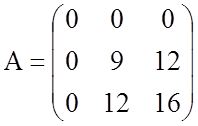Поверхности второго порядка. Канонические уравнения поверхностей второго порядка, страница 2

      .

Ее характеристический многочлен

     

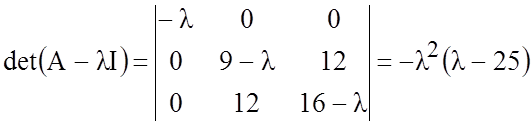
имеет корни . При каждом  будем строить фундаментальную систему решений систем уравнений  и ортонормировать их.

      При  это система имеет вид

     

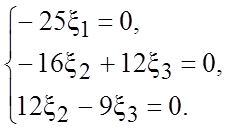
Ее общее решение 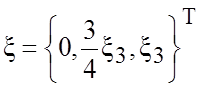 имеет одну свободную переменную. Поэтому фундаментальная система решений состоит из одного решения, например, из решения . Нормируя его, получим .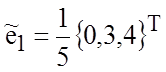

      При  рассматриваемая система имеет вид

     

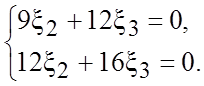
Ее общее решение 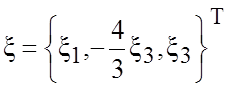 имеет две свободные переменные. Поэтому, фундаментальная система решений состоит из двух решений, например, из решений  и . Поскольку  и  выбраны ортогональными друг к другу (в противном случае требовалось применение процедуры ортогонализации Грама - Шмидта), то остается их лишь нормировать. После нормировки получим .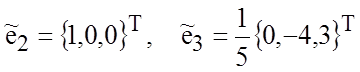

      Из столбцов координат векторов  составим матрицу перехода Р к новому ортонормированному базису

     

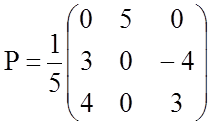
и сделаем проверку

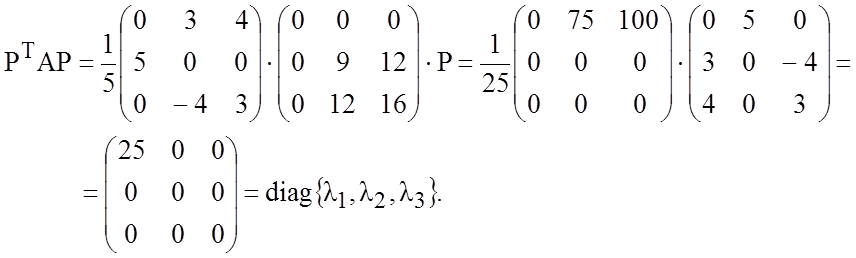
      Выполним преобразование координат

     

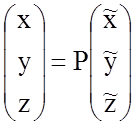
и запишем уравнение данной поверхности в новой прямоугольной системе координат со старым центром О и направляющими векторами :

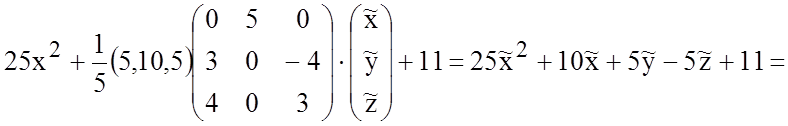
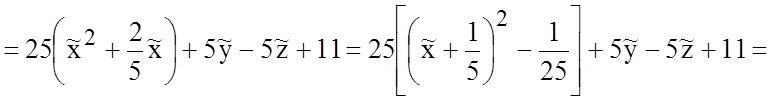
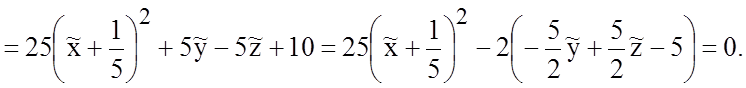
      Теперь совершим преобразование координат, полагая

      ,

      ,

      .

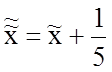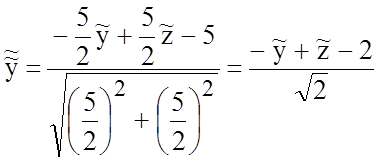При этом коэффициенты  выберем так, чтобы матрица формул рассматриваемого преобразования координат была ортогональной, т.е. чтобы вектор – строки

     

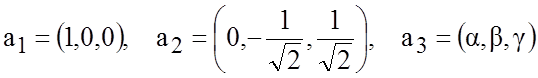
составляли ортонормированную систему векторов. Так как система векторов  ортонормированная, то координаты вектора  следует искать из условий

     

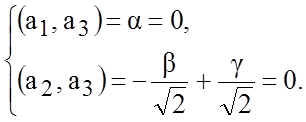
Затем найденный вектор  нужно еще нормировать.

      Проделав это, получим .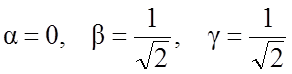

      Следовательно, формулы рассматриваемого преобразования координат имеют вид

      ,

      ,

     

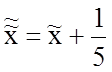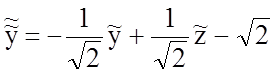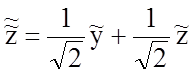
или

      ,

      ,

      .

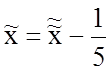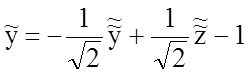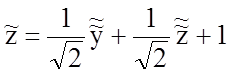В новых координатах рассматриваемая поверхность имеет уравнение

   

        

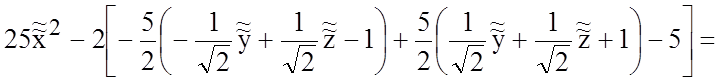
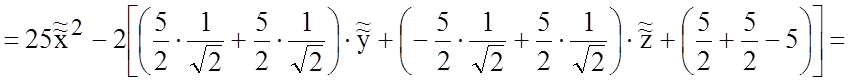
или

      .

Это – каноническое уравнение параболического цилиндра в прямоугольной системе координат .

      Поскольку

      

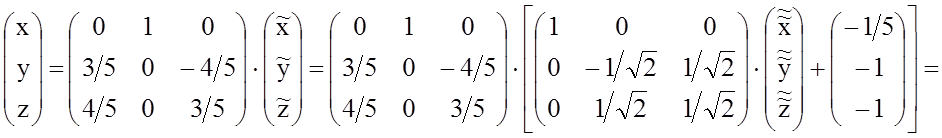
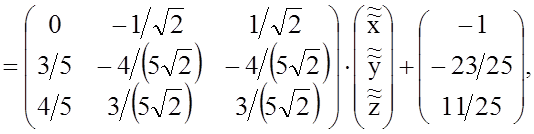
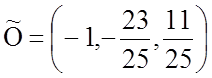каноническая система координат  имеет начало  и

направляющие векторы , ,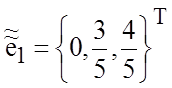

. 

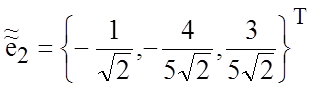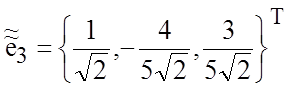      В задачах этого параграфа рассматриваются только прямоугольные системы координат.

      8.5.1. Семейство поверхностей задано уравнением, содержащим произвольный параметр l. Определите тип поверхности при всевозможных l:

      а) ;                                      з) ;           

      б) ;                                    и) ;          

      в) ;                                    к) ;          

      г) ;                                       л) ;          

      д) ;                                       м) ;          

      е) ;                                   н) ;          

      ж) ;                                  о) .          

      8.5.2. а) Сечения поверхности  плоскостями , ,  спроектированы на плоскость Oyz. Изобразите проекции.

      б) Сечения поверхности  плоскостями , ,  спроектированы на плоскость Oyz. Изобразите проекции.

      в) Сечения поверхности  плоскостями , ,  спроектированы на плоскость Oyz. Изобразите проекции.

      г) Сечения поверхности  плоскостями , ,  спроектированы на плоскость Oxz. Изобразите проекции.

      д) Сечения поверхности  плоскостями , ,  спроектированы на плоскость Oxy. Изобразите проекции.

      8.5.3. а) Сечения поверхностей ,  ,  плоскостью  спроектированы на плоскость Oyz. Изобразите проекции.

      б) Сечения тех же поверхностей плоскостью  спроектированы на плоскость Oxy. Изобразите проекции.

      8.5.4. По какой линии плоскость  пересекает следующую поверхность:

      а) ;                 г) ;

      б) ;                    д) .

      в) ;

      8.5.5. Установите, что плоскость  пересекает эллипсоид 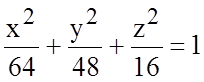 по эллипсу, и найдите его вершины и полуоси.

      8.5.6. Найдите параметр и вершину параболы, получающейся в пересечении плоскости  и гиперболического параболоида .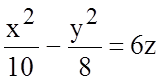

      8.5.7. Покажите, что плоскость  пересекает однополостный гиперболоид 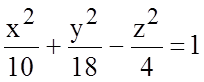 по гиперболе. Найдите полуоси и вершины этой гиперболы.

      8.5.8. Приведите уравнения к каноническому виду при помощи перехода к новой прямоугольной системе координат и выясните расположение относительно исходной прямоугольной системы координат следующих поверхностей второго порядка:

      а) ;

      б) ;

      в) ;

      г) ;

      д) ;

      е) ;

      ж) ;

      з) ;

      и) ;

      к) ;

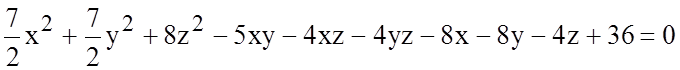      л) ;

      м) ;

      н) ;

      о) ;

      п) ;

      р) .