Методы линеаризации уравнений

Методы линеаризации уравнений

1.  Нелинейная функция является аналитической в рабочей области и ее можно разложить в ряд Тейлора.

Математическое описание элементов удобно выполнять через переменные состояния. В этом случае их динамику можно представить в виде системы уравнений 1-го порядка относительно этих переменных. При такой форме описание элементов переменные состояния аналогичны обобщенным координатам, а пространство их изменения является фазовым. Состояние элемента в любой текущий момент времени характеризуется совокупностью фазовых координат, которые можно объединить в вектор состояния и представить их описание в векторной форме (математической модели).

Простейшим методом исследования нелинейных систем является линеаризация. Суть ее состоит в том, что нелинейная система заменяется эквивалентной линейной. Очевидно, что линеаризованная модель не может полностью заменить нелинейную систему, но в некотором смысле поведение линеаризованной модели оказывается идентичным поведению нелинейной модели. Т.е. имеется возможность применить некоторые хорошо разработанные методы анализа линейных систем для изучения линеаризованных.

Обычно при описании элементов непрерывного действия используются переменные состояния x(t), связанные с выходными  y(t) и входными  сигналами с помощью следующих уравнений:

=;

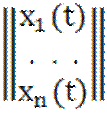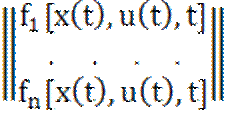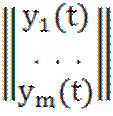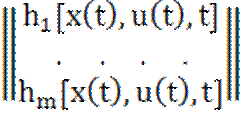                                     = .                           (1.1)

Уравнения (1.1) справедливы на интервале времени (,T], при заданных начальных условиях  x().

Будем считать систему уравнений (1.1) нелинейной, если в ней переменные состояния присутствуют не только в линейной форме, но и в виде произведений, целой (дробной) степени координат и трансцендентных функций от них. Во многих элементах нелинейную зависимость часто не удается выразить в аналитической форме, тогда ее представляют графиками или в виде таблиц.

Линеаризуем (1.1) по этому методу при условии малости приращений относительно положения равновесия  f(=0, т.е.

 ;

                                               .                              (1.2)

Тогда 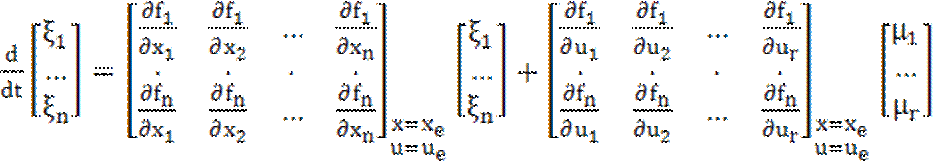    (1.3)

Из второго уравнения системы (1.1) получим

                  .                  (1.4)

Поэтому

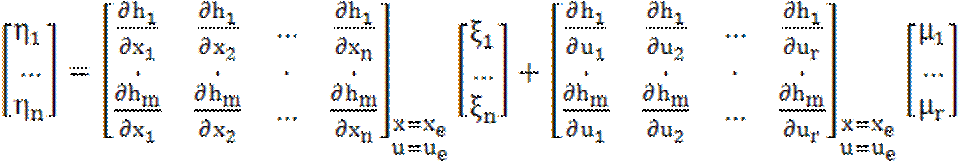 (1.5)             

Если провести линеаризацию относительно опорной траектории программного движения с параметрами x(t)=; y(t)= u(t)=(t), то

 ;

                                        .                                  (1.6)

При этом 

(t)=(t)+(t)=

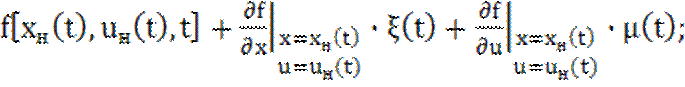
(t)=(t)+𝜂(t)=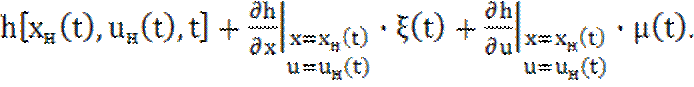

Подчеркнем, что в этом случае матрицы

,   ,    ,   

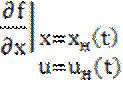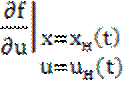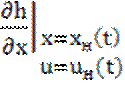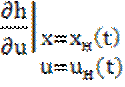
зависят от t.

Отсюда следует, что

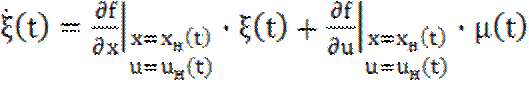                                                       (1.7)

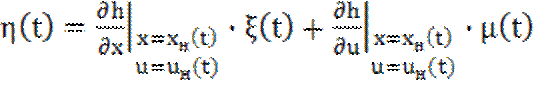                                                      (1.8)

Пример. Уравнения углового движения искусственного спутника Земли при действии на него моментов силы тяги u(t) относительно его главных осей инерции можно записать в форме Эйлера:

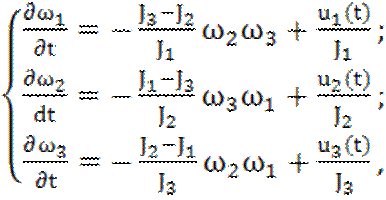                                                                (1.9)

где , ,(i=1,2,3) –соответственно, составляющие момента инерции, угловой скорости и управляющего момента относительно одной из главных осей  ИСЗ.

Система уравнений (1.9) нелинейна из-за наличия в выражениях правых частей произведений угловых скоростей.

Линеаризуем систему уравнений (1.9) с помощью первого метода. Введем обозначения

;   ;   .

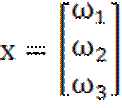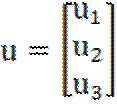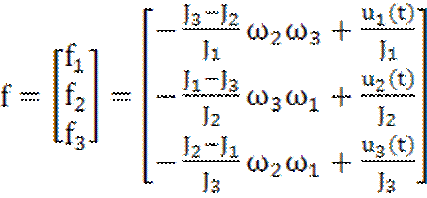Составим матрицы

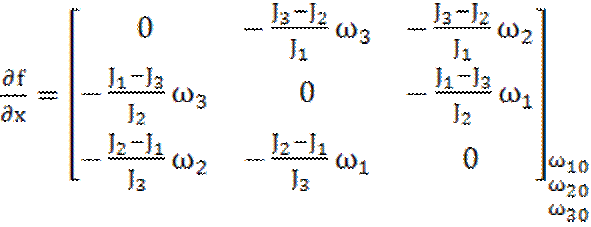                                             (1.10)

и

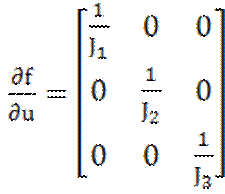                                                  .                                        (1.11)

Запишем уравнение (1.9) в линеаризованном виде с учетом выражений (1.10) и (1.11):

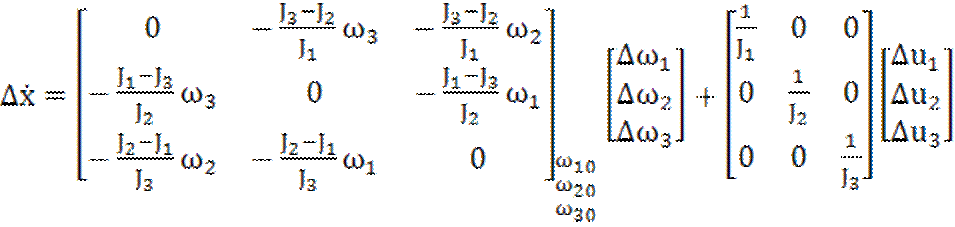 (1.12)                                       

2.  Нелинейные характеристики не могут быть описаны математически, а задаются в графической форме соответствующими зависимостями y=M(x).

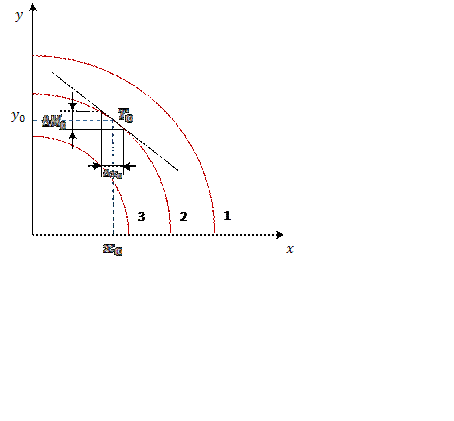
                                    Графическая форма нелинейных  характеристик

                                 элемента при режимах работы, заданных кривыми 1-3.

В этом случае производят графическую линеаризацию характеристики 2 в рабочей точке  с координатами (, т.е. кривая заменяется касательной. Тогда вместо частных производных находят частные разности  и можно записать следующее соотношение

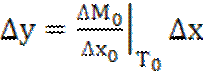                                  .                                                  (1.13)

Пользуясь соотношением (1.13), коэффициент усиления можно представить в виде

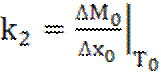                                  .                                                       (1.14)

Таким образом, получим линеаризованное уравнение

                                  .                                                         (1.15)

3.  Вместо непосредственного определения частных производных вводим переменные в исходные нелинейные уравнения. Эти переменные имеют вид:

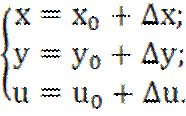                                                                                       (1.16)

Следует помнить, что приращения переменных всегда зависят от времени t. Все слагаемые, стоящие в правых частях полученных выражений, разобьем на три группы: не содержащие приращения  и  в виде простых множителей; содержащие произведения или степени приращений. Полагая приращения  и  малыми по сравнению с соответствующими координатами опорной траектории , можно считать слагаемые третьей группы практически равными нулю. Слагаемые первой группы будут определять опорное движение, а слагаемые второй – движение в отклонениях () от опорной траектории .

Примеры

1).  Уравнение устройства для замера угловых скоростей вращения выходного вала двигателя внутреннего сгорания или турбин можно записать в виде

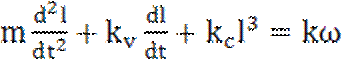                              ,                               (1.17)

где   – перемещение устройства массы m для замера угловых скоростей;  - коэффициент скоростного трения; − коэффициент жесткости пружины; – коэффициент пропорциональности при угловой скорости вращения выходного вала двигателя или турбины .

Линеаризуем с помощью третьего способа уравнение (1.17), подставив в него

 и ,

где   и   - постоянные. В результате получим

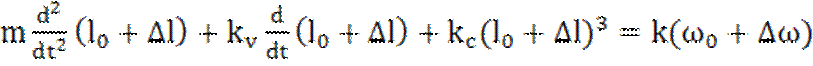    .    (1.18)

Из уравнения (1.18) можно получить две зависимости: для опорного движения

и в приращениях 

                                      .                          (1.19)

Уравнение (1.19) является линейным.

2).  Уравнение ракеты, вертикально стартующей под действием силы тяги, будет

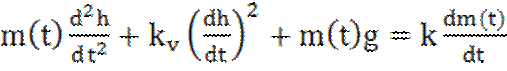                           ,                   (1.20)

где  – высота полета ракеты;  – переменная масса ракеты;  – постоянные коэффициенты;  – ускорение свободного падения.

Линеаризуем уравнение (1.20) относительно опорной траектории вертикального взлета, т.е.

, .

Подставив эти соотношение в уравнение (1.20), запишем

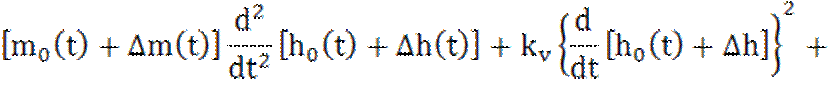
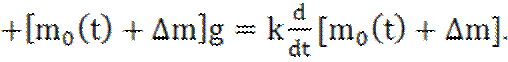                                                        (1.21)

Из уравнения (1.21) можно получить две зависимости: относительно опорной траектории

и в приращениях

              .   (1.22)

Уравнение (1.22) является линейным.

4.  МНК.