Для невырожденного оператора существует обратный
оператор для В, такой что АВ=ВА=I. Т.к. при
перемножении линейных операторов их матрицы перемножаются, а тождественный
оператор имеет единичную матрицу, то матрица обратного оператора ![]() =
=![]() .
.
Преобразование матрицы линейного оператора при изменении базиса
A:X![]() Y,
dimX=n, dimY=m
Y,
dimX=n, dimY=m
P
![]()
е![]() ,е
,е![]() ,
,![]() ,е
,е![]() - первый
базис в X, f
- первый
базис в X, f![]() ,f
,f![]() ,…,f
,…,f![]() - второй базис в X
- второй базис в X
![]()
![]()
![]() A
A![]()
![]()
![]() A
A![]()
g![]() ,g
,g![]() ,…,g
,…,g![]() - первый базис в Y, h
- первый базис в Y, h![]() ,h
,h![]() ,
,![]() ,h
,h![]() -
второй базис в Y
-
второй базис в Y

Q
![]() .
.
Коэффициенты
![]() определяют матрицу
определяют матрицу
P=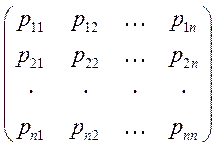 ,
,
называемую матрицей
преобразования координат при переходе от базиса е![]() , е
, е![]() ,
,![]() ,е
,е![]() к
базису f
к
базису f![]() , f
, f![]() ,…,f
,…,f![]() .
.
Возьмем
произвольный вектор x![]() X и
разложим его по векторам обоих базисов, т.е.
X и
разложим его по векторам обоих базисов, т.е. 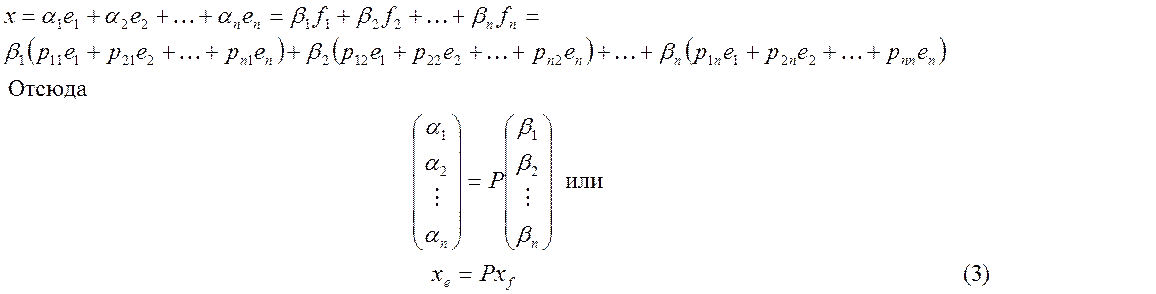
Матрица преобразования координат P в
соотношении (3) невырожденная, т.к. в противном случае имела бы место
линейная зависимость между ее столбцами и, следовательно, между векторами f![]() , f
, f![]() ,…,f
,…,f![]() .
.
Пусть
![]() ,
(4)
,
(4)
![]() ,
(5)
,
(5)
где![]() – матрицы оператора в базисах
– матрицы оператора в базисах ![]() и
и ![]() .
.
Обозначим
через P матрицу преобразования координат при переходе от
базиса е![]() ,е
,е![]() ,
,![]() ,е
,е![]() к базису
f
к базису
f![]() , f
, f![]() ,…,f
,…,f![]() , через Q – матрицу
преобразования координат при переходе от g
, через Q – матрицу
преобразования координат при переходе от g![]() , g
, g![]() ,…,g
,…,g![]() к h
к h![]() , h
, h![]() ,
,![]() ,h
,h![]() , тогда
, тогда
![]() (6)
(6)
и
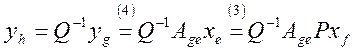 .
.
Сравнивая полученное выражение с (5), заключаем, что
![]() (7)
(7)
Рассмотрим A:X![]() X. Пусть
X. Пусть
е![]() ,е
,е![]() ,
,![]() ,е
,е![]() - первый базис X, f
- первый базис X, f![]() ,f
,f![]() ,…,f
,…,f![]() - второй базис X.
- второй базис X. ![]()
P
x![]() =
= , y
, y![]() =
=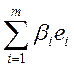 .
.
Тогда
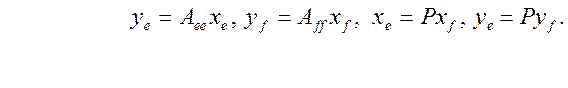
Следовательно ![]() ,
,
т.е.
![]() (7')
(7')
Эквивалентные и подобные матрицы
Две прямоугольные матрицы A и B одинаковых размеров называются эквивалентными, если существует две невырожденные квадратные матрицы R и S, такие что
B=RAS.
Из соотношения (7) следует, что две матрицы, соответствующие одному и тому же линейному оператору в различных базисах пространств X и Y эквивалентны между собой. Справедливо и обратное: если матрица A отвечает оператору A в некоторых базисах пространств X и Y, а матрица B эквивалентна матрице A, то она отвечает тому же линейному оператору в некоторых других базисах X и Y.
Таким образом, каждому линейному оператору, отображающему X в Y, соответствует класс эквивалентных матриц.
Теорема (Критерий эквивалентности матриц).Для того чтобы две прямоугольные матрицы одинаковых размеров были эквивалентны, необходимо и достаточно, чтобы они имели один и тот же ранг.
Доказательство:
Необходимость. При умножении любой матрицы на какую-либо невырожденную матрицу ее ранг не меняется.
![]() , rg C
, rg C ![]() rg A,
rg A, ![]() , rg A
, rg A![]() rg C.
rg C.
Ранг произведения двух прямоугольных матриц не превосходит ранга любого из сомножителей.
Можно показать и обратное, т.е., что матрицы одинаковых рангов эквивалентны. Докажем большее, что всякая матрица ранга r эквивалентна матрице
I
Достаточность. Пусть
дана прямоугольная матрица размером m![]() n. Она
определяет некоторый линейный оператор A, отображающий
пространство X с базисом е
n. Она
определяет некоторый линейный оператор A, отображающий
пространство X с базисом е![]() , е
, е![]() ,
,![]() ,е
,е![]() в пространство Y с базисом g
в пространство Y с базисом g![]() , g
, g![]() ,…,g
,…,g![]() . Обозначим через r число линейно-независимых векторов среди образов
векторов базиса Ae
. Обозначим через r число линейно-независимых векторов среди образов
векторов базиса Ae![]() , Ae
, Ae![]() ,…, Ae
,…, Ae![]() . Не
нарушая общности, можно считать, что линейно-независимыми являются векторы Ae
. Не
нарушая общности, можно считать, что линейно-независимыми являются векторы Ae![]() , Ae
, Ae![]() ,…, Ae
,…, Ae![]() , (иначе можно векторы базиса перенумеровать).
Остальные векторы Ae
, (иначе можно векторы базиса перенумеровать).
Остальные векторы Ae![]() , Ae
, Ae![]() ,…, Ae
,…, Ae![]() линейно
через них выражаются:
линейно
через них выражаются:
![]() . (8)
. (8)
Определим
в линейном пространстве X новый базис f![]() , f
, f![]() ,…,f
,…,f![]() следующим образом:
следующим образом:
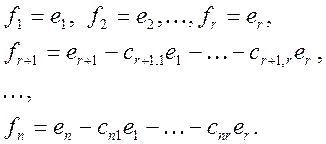
Тогда
![]() (9)
(9)
Положим теперь
![]() (10)
(10)
Векторы h![]() , h
, h![]() ,
,![]() ,h
,h![]() по предположению линейно независимы. Дополним их некоторыми
векторами h
по предположению линейно независимы. Дополним их некоторыми
векторами h![]() ,
,![]() ,h
,h![]() до
базиса пространства Y и
рассмотрим матрицу оператора A в новых базисах f
до
базиса пространства Y и
рассмотрим матрицу оператора A в новых базисах f![]() , f
, f![]() ,…,f
,…,f![]() и h
и h![]() , h
, h![]() ,
,![]() ,h
,h![]() .
.
Коэффициенты
i-го столбца этой матрицы совпадают с координатами
вектора ![]() в базисе h
в базисе h![]() , h
, h![]() ,
,![]() ,h
,h![]() . Согласно
соотношениям (9), (10) матрица оператора A будет
совпадать с I
. Согласно
соотношениям (9), (10) матрица оператора A будет
совпадать с I![]() . Т.к.
матрицы A и I
. Т.к.
матрицы A и I![]() соответствуют
одному и тому же оператору, они эквивалентны.
соответствуют
одному и тому же оператору, они эквивалентны.
Все прямоугольные матрицы размером m![]() n ранга
rэквивалентны
матрице I
n ранга
rэквивалентны
матрице I![]() и,
следовательно, эквивалентны между собой.
и,
следовательно, эквивалентны между собой.
Пусть теперь оператор A действует в пространстве X.
Определение: матрица A называется подобной матрице B, если существует такая невырожденная матрица P, что
![]() ,
,
отсюда
![]() ,
,
т.е. если A подобна B, то и B подобна A. Если
![]() ,
, ![]() ,
,
то
![]() .
.
Поскольку признак подобия удовлетворяет условиям рефлексивности, симметричности и транзитивности, он является отношением эквивалентности.
Заметим, что:
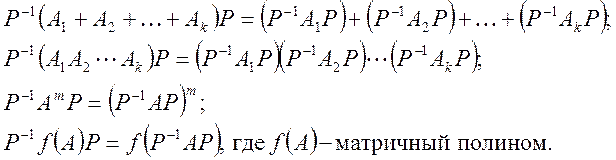
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.