4. Линейное свойство определителя.
a) Если все элементы j-го столбца определителя D представлены в виде
![]() (i=1,2,…,n),
(i=1,2,…,n),
где λ и µ числа из поля F, то
![]() ,
,
причем у определителей ![]() и
и ![]() все столбцы, кроме j-го, такие же,
как у определителя D, а j-й столбец состоит у определителя
все столбцы, кроме j-го, такие же,
как у определителя D, а j-й столбец состоит у определителя ![]() из чисел
из чисел ![]() , у определителя
, у определителя ![]() – из чисел
– из чисел ![]() .
.
Доказательство. Действительно, любой член определителя D можно представить в виде
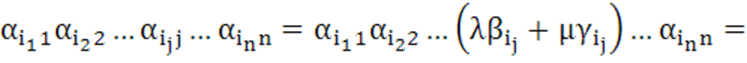
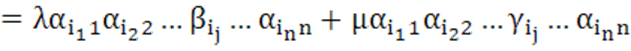 .
.
Отсюда следует, что
![]() .
.
Для того, чтобы
записать в удобном виде обобщение линейного свойства, обозначим через ![]() определитель, который получается при замене
элементов j-го столбца
определителя D на числа
определитель, который получается при замене
элементов j-го столбца
определителя D на числа ![]() . Тогда свойство 4а) можно записать так
. Тогда свойство 4а) можно записать так
![]() ).
).
b) Обобщение линейного свойства:
если каждый элемент j-го столбца есть линейная комбинация
![]() ,
,
то
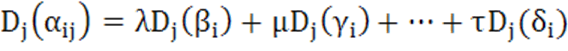 .
.
5. Общий множитель всех элементов некоторого столбца можно выносить за знак определителя.
Доказательство. Из свойства 4
следует, что если ![]() , то
, то
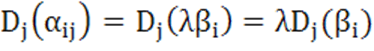 .
.
6. Если некоторый столбец определителя состоит из нулей, то D=0.
Доказательство.
![]() .
.
7. Инвариантность определителя к линейному комбинированию столбцов.
a) Определитель не изменится, если к элементам одного из его столбцов прибавить соответствующие элементы любого другого столбца, умноженные на фиксированное число.
Доказательство. Действительно,
пусть к j-му столбцу
прибавляется k-й ![]() , умноженный на число λ. Тогда имеем:
, умноженный на число λ. Тогда имеем:
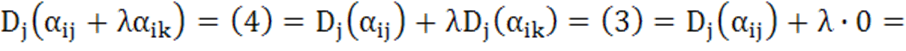
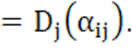
b) Обобщение: определитель не
изменится, если к элементам его j-го столбца прибавить соответствующие
элементы k-го столбца,
умноженные на число λ, затем элементы l-го столбца, умноженные на число
µ, … , элементы p-го столбца, умноженные на число τ ![]() .
.
8. Все свойства, доказанные для столбцов определителя, остаются справедливы и для его строк.
9. ![]() .
.
Алгебраические дополнения и миноры.
Рассмотрим произвольный, например, j-й, столбец определителя D:
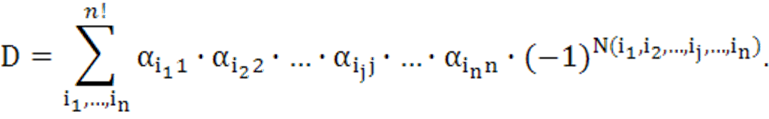
Соберем в правой
части все слагаемые, содержащие ![]() , и вынесем эти элементы за скобки. Получим:
, и вынесем эти элементы за скобки. Получим:
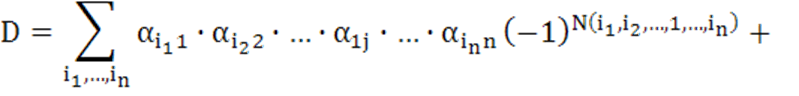
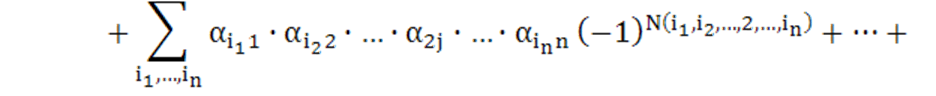
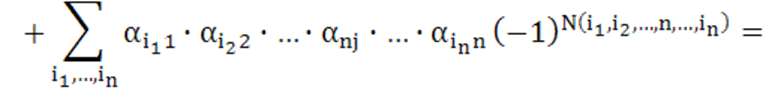
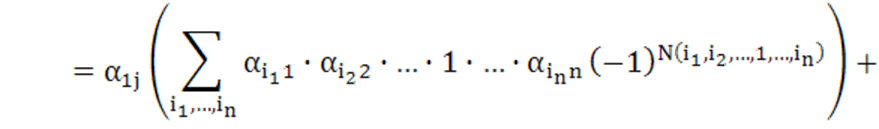
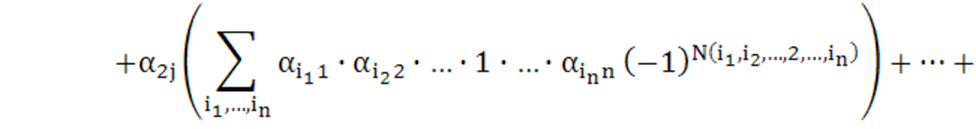
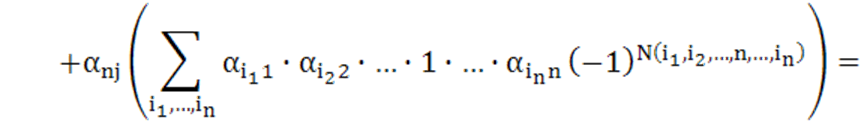
![]() (
(![]() )
)
Здесь мы
обозначим через ![]() величину, стоящую в i-ой скобке; она
называется алгебраическим дополнением элемента
величину, стоящую в i-ой скобке; она
называется алгебраическим дополнением элемента ![]() в определителе D. Полученная
формула называется формулой разложения определителя D по элементам j-го столбца.
в определителе D. Полученная
формула называется формулой разложения определителя D по элементам j-го столбца.
Аналогично выводится формула разложения определителя по элементам i-ой строки:
![]() (
(![]() )
)
Таким образом, справедлива следующая
Теорема 1. Сумма всех произведений элементов какого-либо столбца (или строки) определителя D на соответствующие алгебраические дополнения равна самому определителю D.
Теорема 2. Сумма всех произведений элементов какого-либо столбца (или строки) определителя D на алгебраические дополнения элементов другого столбца (строки) равна нулю.
Доказательство. Заменим в правой
и левой частях равенства (![]() ) элементы
) элементы ![]() на соответствующие элементы какого-либо другого,
например k-го, столбца.
Тогда определитель слева в (
на соответствующие элементы какого-либо другого,
например k-го, столбца.
Тогда определитель слева в (![]() ) будет иметь два одинаковых столбца и, по свойству
3, будет равен нулю, т.е. при
) будет иметь два одинаковых столбца и, по свойству
3, будет равен нулю, т.е. при ![]()
![]()
Такими же
рассуждениями при ![]() из формулы (
из формулы (![]() ) получаем
) получаем
![]()
Если зачеркнуть
в матрице n-го порядка i-ю строку и j-й столбец, то
оставшиеся элементы образуют некоторую матрицу (![]() )-го порядка, определитель которого называется минором
и обозначается
)-го порядка, определитель которого называется минором
и обозначается ![]() .
.
Теорема3.Справедлива формула
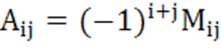 .
.
Доказательство.Пусть i=1, j=1. Соберем в правой части равенства
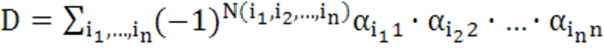
все
члены, содержащие ![]() , и вынесем
, и вынесем ![]() за скобки. Будем иметь:
за скобки. Будем иметь:
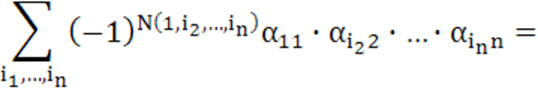
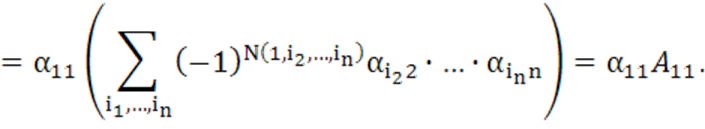
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.