Методы проверки гипотез о законах распределения и параметрах законов распределения (Раздел 7 учебного пособия "Статистические методы обработки экспериментальных данных")

7. методы проверки гипотез о законах распределения и параметрах законов распределения

7.1. Проверка гипотез о законах распределения

7.1.1. Выравнивание статистических рядов

При обработке экспериментальных данных одним из основных вопросов является обоснование закона распределения исследуемой случайной величины.

Пусть экспериментальным путём получена случайная выборка , ,…,. В связи с её ограниченностью при обработке статистического материала приходится решать две задачи.

1. Подобрать для полученного статистического ряда теоретическую кривую распределения, выражающую лишь существенные черты статистического материала, но не случайности, связанные с недостаточным объёмом экспериментальных данных (задача выравнивания или сглаживания статистических рядов).

2. Определить, чем объясняются неизбежные расхождения между подобранной теоретической кривой распределения и статистическим распределением: случайными обстоятельствами или тем, что подобранная кривая неудовлетворительно выравнивает данное статистическое распределение (задача проверки гипотезы о законах распределения).

Процедура выравнивания заключается в том, чтобы подобрать теоретическую кривую распределения, с той или иной точки зрения наилучшим образом описывающую данное статистическое распределение.

Задача о наилучшем выравнивании статистических рядов, как и вообще задача о наилучшем аналитическом представлении эмпирических функций, является в значительной мере неопределённой, и решение её зависит от того, что условиться считать «наилучшим». Например, при сглаживании эмпирических зависимостей часто используют метод наименьших квадратов (раздел 8), согласно которому наилучшим приближением к эмпирической зависимости в данном классе функций является такое, при котором сумма квадратов отклонений обращается в минимум. При этом вопрос о том, в каком именно классе функций следует искать наилучшее приближение, решается уже не из математических соображений. Вид функции, выражающей исследуемую зависимость часто известен заранее. Из опыта требуется получить лишь некоторые численные параметры, входящие в выражение функции. Именно эти параметры подбираются с помощью метода наименьших квадратов.

Аналогично обстоит дело и с задачей выравнивания статистических рядов. Как правило, вид теоретической кривой выбирается заранее из соображений, связанных с существом задачи, а в некоторых случаях просто с внешним видом статистического распределения. Аналитическое выражение выбранной кривой распределения зависит от некоторых параметров. Поэтому задача выравнивания статистического ряда переходит в задачу рационального выбора тех значений параметров, при которых соответствие между статистическим и теоретическим распределениями оказывается наилучшим.

Следует иметь в виду, что любая аналитическая функция f(x), с помощью которой выравнивается статистическое распределение, должна обладать основными свойствами плотности распределения:

                                           f(x) ³ 0; 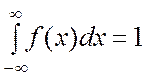   .              (7.7.1)

Предположим, что исходя из тех или иных соображений выбрана теоретическая кривая распределения , удовлетворяющая условиям (7.1.1). С помощью данной кривой требуется выровнять данное статистическое распределение. В выражение функции  входят параметры (a₁, a₂,…,a_m) ^Т = A_<m>,  т.е.

                                              .                (7.1.2)

Необходимо подобрать эти параметры так, чтобы кривая (7.1.2) наилучшим образом описывала данный статистический материал. Один из методов, применяемых для решения данной задачи – метод моментов.

Согласно методу моментов параметры выбираются с таким расчётом, чтобы несколько важнейших числовых характеристик (моментов) теоретического распределения были равны соответствующим статистическим характеристикам. Например, если теоретическая кривая зависит только от двух параметров:

                                               ,

эти параметры выбираются так, чтобы математическое ожидание  и дисперсия  теоретического распределения совпадали с соответствующими статистическими характеристиками  и . Если кривая  зависит от трёх параметров, можно подобрать их так, чтобы совпали первые три момента, и т.д.

П р и м е р 7.1. Произведено 500 измерений отклонения по вертикали при стрельбе в мишень. Результаты измерений сведены в статистический ряд, табл.7.1. Требуется выровнять данное распределение с помощью нормального закона.

Таблица 7.1

Интервальный статистический ряд (к примеру 7.1)