Методы проверки гипотез о законах распределения и параметрах законов распределения (Раздел 7 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 6

                                                   ,                      (7.2.2)

которая, очевидно, распределена по нормальному закону и имеет числовые характеристики:

                    ;    ;     .

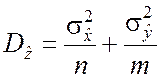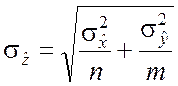Нормируем случайную величину (7.2.2) и получаем

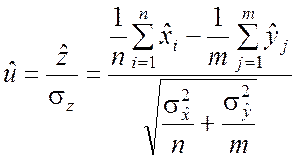                                         .            (7.2.3)

Случайная величина (7.2.3) подчинена нормальному закону распределения, параметры которого известны:  = 0,   = 1, что существенно упрощает процедуру проверки нулевой гипотезы. Действительно, если гипотеза H₀ справедлива ( = ), то случайная величина  центрирована, откуда следует, что  = 0. Так как выборки независимые, то  = 1.

Критическая область строится в зависимости от вида конкурирующей гипотезы, которая может быть сформулирована тремя различными способами:

                                   ¹ ;   > ;   < .

Рассмотрим методику проверки гипотезы H₀ для каждого из приведённых способов формулировки конкурирующей гипотезы.

1. H₀:  = ;     H₁:  ¹ .

В этом случае  строят двустороннюю критическую область, исходя из требования, чтобы вероятность попадания в неё показателя согласованности в предположении о справедливости нулевой гипотезы была равна принятому уровню значимости a.

Наибольшая мощность критерия достигается тогда, когда левая и правая критические точки u_a1, u_a2 выбраны так, что вероятность попадания показателя согласованности  в каждый из двух интервалов критической области равна a/2:

                                  ;     .

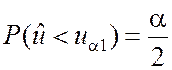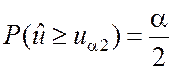Поскольку  – нормированная нормально распределённая случайная величина и её распределение симметрично относительно нуля, то критические точки также симметричны относительно нуля:

                                                 |u_a1| = |u_a2| = |u_a|.

Используя функцию нормированного нормального распределения (функцию Лапласа), вероятность попадания показателя согласованности в критическую область можно определить выражением

                                    ,

откуда

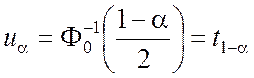                                            .               (7.2.4)

Двусторонняя критическая область будет определяться неравенствами u < –u_a,  u > u_a. Таким образом, правило проверки гипотезы H₀ для рассматриваемого случая состоит в следующем.

а). Назначается уровень значимости a и в соответствии с формулой (7.2.4) по таблице приложения 4 определяются границы критической области  u_a1 = –u_a,   u_a2 = u_a.

б). На основе случайных выборок вычисляется наблюдаемое значение показателя u по формуле

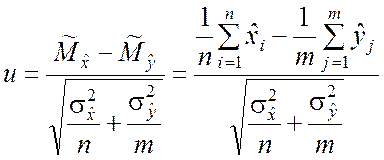                                   .     (7.2.5)

в). Проверяется условие |u| > u_a. Если оно выполняется, то гипотеза H₀ отвергается. В противном случае данные эксперимента не противоречат нулевой гипотезе.

П р и м е р 7.4. Производится контрольный отстрел двух партий снарядов, причём из первой партии проверяется 10 снарядов, а из второй – 15. В результате отстрела получены следующие оценки математических ожиданий отклонения точек попадания снарядов от точки прицеливания по дальности: для первой партии отклонение равно –0,8 км, для второй +0,4 км. Среднеквадратические отклонения по дальности для снарядов первой и второй партий известны и равны соответственно 2 и 1,5 км. Необходимо проверить гипотезу о совпадении проекций центров рассеивания на ось дальности в обеих партиях.

▼ Пусть  и  – отклонение точек попадания снарядов от точки прицеливания по дальности соответственно для первой и второй партий.

По условию задачи n = 10, m = 15,  = –0,8 км,  = 0,4 км,  = 2 км,  = 1,5 км.

Задаёмся уровнем значимости a = 0,05 и в приложении 4 находим

                                          u_a = t_1–a = t_g = t_0,95 = 1,96.

Используя формулу (7.2.5), вычисляем абсолютное значение показателя согласованности:

                                           .                       

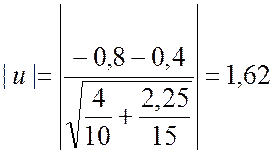Так как |u| < u_a, нулевая гипотеза   =  не противоречит данным контрольного отстрела.