Методы проверки гипотез о законах распределения и параметрах законов распределения (Раздел 7 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 5

Существенное достоинство метода К. Пирсона состоит в возможности его применения тогда, когда априорно известен лишь вид гипотетического распределения, но не известны его параметры. В этом случае параметры распределения заменяются оценками, которые используются в дальнейшем для вычисления вероятностей p_l, а число степеней свободы уменьшается на число заменяемых параметров. Метод К. Пирсона имеет следующие недостатки:

а) он применим только при большой выборке (n ³ 100), так как показатель согласованности подчиняется распределению хи-квадрат лишь при достаточно большом n;

б) результаты проверки в значительной степени зависят от способа разбиения выборки на интервалы, причём их число целесообразно делать не менее 8–10, а количество попаданий случайной величины  в любой из интервалов должно быть не менее 5.

П р и м е р 7.3. В условиях примера 7.1 проверить согласованность теоретического и статистического распределений.

▼ Назначаем уровень значимости a = 0,05. Число степеней свободы  f = 8 – 3 = 5. По таблице приложения 7 определяем критическую границу u_0,05 = 11,1.

Пользуясь теоретическим нормальным законом распределения с параметрами   m = 0,168 и   s = 1,448,   находим вероятности попадания в разряды по формуле

                                    ,

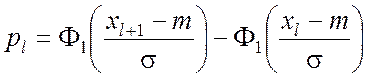где x_l,  x_l+1 – границы l-го разряда.  Значения функции Ф₁ находим в таблице приложения 3.  Затем составляем расчётную таблицу 7.3.

Таблица 7.3

Расчётные данные (к примеру 7.3)

Jl	–4; –3	–3; –2	–2; –1	–1; 0	0; 1	1; 2	2; 3	3; 4
	0,012	0,050	0,144	0,266	0,240	0,176	0,092	0,020
pl	0,012	0,052	0,142	0,244	0,264	0,181	0,076	0,021
	0	–0,002	0,002	0,022	–0,024	–0,005	0,012	–0,001
	0	4∙10–6	4∙10–6	484∙10–6	576∙10–6	25∙10–6	144∙10–6	10–6
	0	0,038	0,014	0,992	1,091	0,069	0,947	0,024

По формуле (7.1.10) находим значение показателя согласованности гипотезы

                                        .

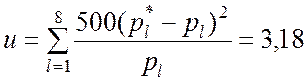Поскольку u = 3,18,  u_0,05 = 11,1,  то u < u_0,05 – гипотеза о нормальном распределении отклонений по вертикали при стрельбе в мишень принимается.                                                                                                ▲

7.2. Проверка гипотез о параметрах законов распределения

7.2.1. Проверка гипотез о равенстве математических ожиданий

Пусть имеются две независимые случайные величины  и , распределённые по нормальному закону. Эксперимент состоит в том, что над случайными величинами  и  осуществляется соответственно n и m независимых испытаний, в результате которых получаются случайные выборки , ,…, и , ,…,. По этим выборкам определяются оценки математических ожиданий

                                     ,     .

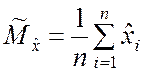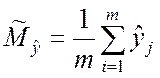Требуется по полученным оценкам проверить гипотезу о равенстве математических ожиданий  и .

Такая задача ставится потому, что, как правило, оценки математических ожиданий оказываются различными. Причина этого может быть двоякой: либо действительно отличны и оценки и математические ожидания, либо  и  одинаковы, а отличие оценок вызвано случайными причинами, в частности, случайным отбором вариантов выборки. Если окажется, что нулевая гипотеза справедлива ( = ), то различие в оценках  и  обусловлено случайными причинами, иначе различными являются математические ожидания. При решении данной задачи  остановимся на том случае, когда дисперсии  и  известны.

В качестве показателя согласованности гипотезы выберем случайную величину

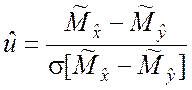                                                 .                   (7.2.1)

Целесообразность выбора показателя согласованности вида (7.2.1) определяется следующими соображениями.

Введём в рассмотрение случайную величину